“Matrices” are a fundamental tool for data science, machine learning, and linear algebra in Python. They store numbers in a grid-like structure and enable various operations such as solving equations and transforming data. Sometimes, we may need to reverse the effect of a matrix by finding its inverse. Inverting a matrix can help us solve a system of linear equations. To inverse a matrix, the “numpy” library is used in Python.
This article explains how to use “numpy” to inverse a matrix using several examples.
What is the Matrix Inverse?
Mathematically, a matrix is an array of rows and columns of num/numbers, symbols, or equations. Inverses of matrices are new matrices that produce the identity matrix by multiplying them with the original given matrices. A square matrix containing “ones” along the diagonal and “zeroes” elsewhere is the identity matrix.
How to Inverse a Matrix Utilizing “numpy”?
The “numpy” library provides a simple function called “inv()” to invert a matrix. This function takes a matrix as its input and returns its inverse.
Syntax
In the above syntax, the “a” parameter corresponds to the matrix to be inverted.
Note: The inverse of a matrix is not applicable/functional to all types of matrices. It is such that if the given matrix is singular, i.e., its determinant is “zero”, it does not have an inverse. In such cases, the “inv()” function will raise a “LinAlgError” exception.
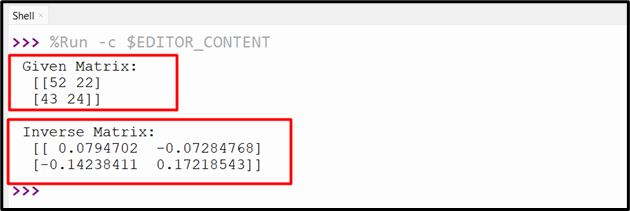
Example 1: Computing Inverse of a “2×2” Matrix
Let’s take a simple “2×2” matrix and compute its inverse using “numpy”:
value_a = numpy.array([[52, 22], [43, 24]])
print('Given Matrix: \n',value_a)
inv_a = numpy.linalg.inv(value_a)
print('Inverse Matrix: \n',inv_a)
In the above code, a “2×2” matrix is created and the “inv()” function of the “numpy.linalg” module is used to compute its inverse.
Output
The output snippet shows the inverse matrix of the given matrix.
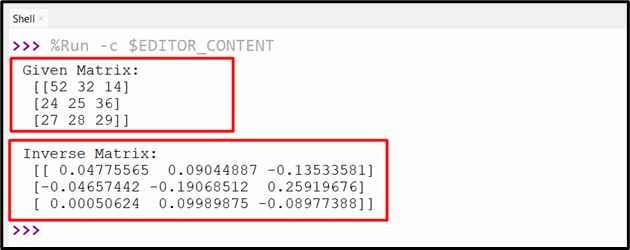
Example 2: Computing Inverse of a “3×3” Matrix
Let’s take a “3×3” matrix and compute its inverse using “numpy”:
value_1 = numpy.array([[52, 32, 14], [24, 25, 36], [27, 28, 29]])
print('Given Matrix: \n',value_1)
inv_1 = numpy.linalg.inv(value_1)
print('\nInverse Matrix: \n',inv_1)
The above code lines created a “3×3” matrix and computed its inverse via the “inv()” function.
Output
The above output returns the inverse of a “3×3” matrix.
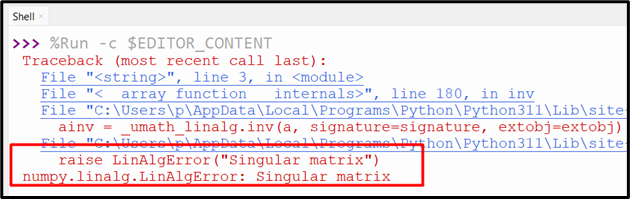
Example 3: Computing Inverse of “Singular Matrix”
Let’s take a singular matrix and try to compute its inverse:
matrx_1 = numpy.array([[1, 2], [2, 4]])
inv_1 = numpy.linalg.inv(matrx_1)
print(inv_1)
In the above code block, the “numpy.linalg.inv()” function takes a singular matrix and returns the error “LinAlgError” upon calculating its inverse.
Output
The above output implies that the inverse of the matrix has not been calculated since the given matrix is singular.
Alternative Approach: Find the Inverse of a Matrix Using the “scipy” Library
The “linalg.inv()” function of the “scipy” library is also used to find the numpy inverse. Let’s understand it via the below example.
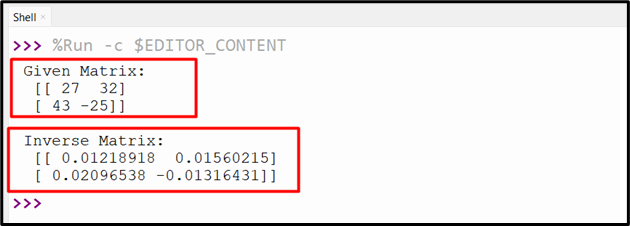
Example
The following code uses the “linalg.inv()” function of the “scipy” library to get the inverse of the matrix:
from scipy import linalg
value_a = numpy.matrix([[27, 32,],[43, -25]])
print('Given Matrix: \n',value_a)
value_b = linalg.inv(value_a)
print('\nInverse Matrix: \n',value_b)
In this code, the “linalg.inv()” function of the “numpy” library is used to find the inverse of the specified matrix.
Output
This outcome returns the inverse matrix of the given matrix.
Conclusion
Matrix inversion is a vital frequent operation in linear algebra, and “numpy” offers a simple function “inv()” for this purpose. This article discussed how to inverse a matrix with “numpy” using the “inv()” function. The “scipy” library comprises a function named “linalg.inv()” that can also be used to find the inverse of the given matrix. Various examples of finding the inverse of matrices are demonstrated with different sizes, including a singular matrix.