Optimization theory and operation research include many mathematical methods to find the maximum and minimum of the objective function but these methods require high calculations that take much time. With MATLAB, it has now become pretty straightforward due to the built-in fminsearch() function that efficiently calculates the minimum of an unconstrained objective function.
This article will elaborate on the functionality of the fminsearch() function in MATLAB.
How to Use the fminsearch() Function in MATLAB?
The fminsearch() is a built-in function in MATLAB that permits us to calculate the minimum of the given unconstrained objective function. This function accepts the functional expression and an initial guess x0 as inputs and provides the minimum of the function as a return value.
The fminsearch() function uses a direct search algorithm for computing the local minimum of the function. It starts the search from the initial starting point, and then iteratively moves to a new point that reduces the function value. Once the algorithm finds a point where the function value cannot be reduced further, it terminates.
Syntax
The fminsearch() function can be implemented in MATLAB through several syntaxes, some of which are given below:
x = fminsearch(fun,x0,options)
x = fminsearch(problem)
Here:
- The function x = fminsearch(fin,x0) is responsible for determining the local minimum x of the given function fun starting from the initial point x0.
- The function x = fminsearch(fun,x0,options) is responsible for determining the local minimum of the given function fun by minimizing with the given optimization options denoted by the structure options.
- The function x = fminsearch(problem) is responsible for determining the minimum of the given problem that is represented by a structure “problem”.
Example 1: How to Find the Minimum of the Rozenbrock’s Function in MATLAB Using the fminsearch() Function
This MATLAB code determines the local minimum of the challenging function Rozenbrock’s starting from the point x0=[-1,0,2] using the fminsearch() function.
x0 = [-1.0,2];
x = fminsearch(fun,x0)
In the above code, the @ is a function handle, which is a pointer to the fun function. The first line of the code defines the objective function, while the initial guess [-1.0,2] is provided as a starting point. We then use the fminsearch() function to get the output of the code, which is the estimated minimum point x and the objective function value.
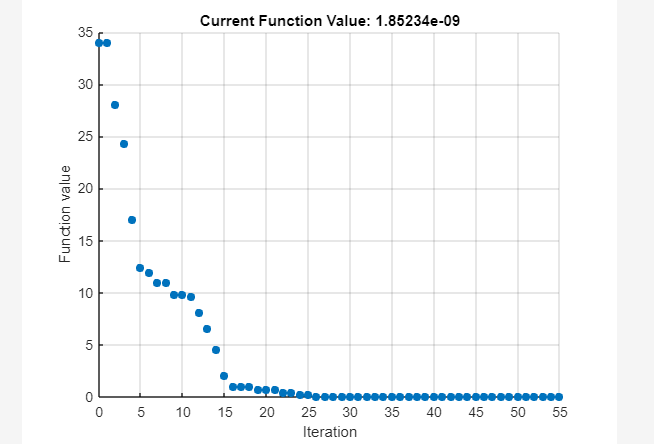
Example 2: How to Monitor the Optimization Process in MATLAB Using fminsearch() Function
In the given example, we use the fminsearch() function to determine the minimum of the function fun starting from the point [-1,0,2]. We also monitor the optimization process using the structure options in the given plot.
x0 = [-1.0,2];
options = optimset('PlotFcns',@optimplotfval);
x = fminsearch(fun,x0,options)
In the above code, besides using the objective function and initial guess as a starting point, we also used the optimization options that control the process of optimization. The PlotFcns is used to specify a custom plot function while the @optimplotfval function is used to monitor the progress of the objective function and see how the value changes over time. The optimization is performed using the fminsearch() function with the options parameter as an additional argument.

Conclusion
Finding the minimum of the unconstrained objective function is an important problem of optimization theory that manually requires many calculations; however, we can perform it in MATLAB more efficiently and accurately using the fminsearch() function. This guide has provided us with a beginner guide to help us understand the workings of the fminsearch() function in MATLAB with some examples.