Matrix polynomials are the polynomials that can be created by an ordinary polynomial by taking their variables in the form of matrices. These polynomials are widely used in many domains of mathematics and engineering.
Evaluating a matrix polynomial is not an efficient task when it is performed manually. But nowadays, it has become an easy task that can be performed in a very short amount of time using MATLAB’s polyvalm() function.
This guide is going to present:
- What is the Matrix Polynomial?
- What are the Applications of the Matrix Polynomial?
- How to Evaluate a Polynomial of a Matrix in MATLAB?
- Example 1: How to Use polyvalm() Function to Evaluate a Polynomial of a Matrix in MATLAB?
- Example 2: How to Use the polyvalm() Function to Evaluate the Characteristic Polynomial of a Matrix in MATLAB?
- Conclusion
What is the Matrix Polynomial?
A matrix polynomial can be defined as a polynomial whose variables are matrices. These polynomials have the following form:
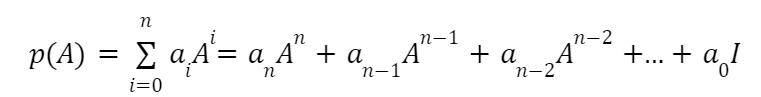
Where,
- p represents a polynomial.
- A represents a square matrix.
- n represents the degree of the polynomial.
- I represents the identity matrix.
Remember that, the dimension of the identity matrix I must be equal to the dimension of the matrix A.
What are the Applications of the Matrix Polynomial?
The matrix polynomials are mostly used in:
- Numerical Analysis
- Differential Equations
- Linear Algebra
- Mechanics
- System Theory
How to Evaluate a Polynomial of a Matrix in MATLAB?
We can evaluate a polynomial of a matrix in MATLAB using the built-in polyvalm() function. This function accepts an ordinary polynomial and a square matrix as parameters and returns a matrix having the same size as the input matrix by evaluating the given polynomial corresponding to the given input matrix.
Syntax
The polyvalm() function can be implemented through the given syntax:
Here,
The function Y=polyvalm(p,X) is responsible for evaluating the polynomial p for the given square matrix X. This process is equivalent to substituting matrix X in the polynomial p where p represents a vector containing the coefficient of the polynomial p in the order of decreasing powers. The value of the polynomial p can be entered by the user or it can be a characteristic polynomial of the given matrix X. If we consider p as a characteristic polynomial, we can find it using the poly() function in terms of the matrix X.
Follow this link to understand the creation of the polynomial p using the poly() function in MATLAB.
Example 1: How to Use polyvalm() Function to Evaluate a Polynomial of a Matrix in MATLAB?
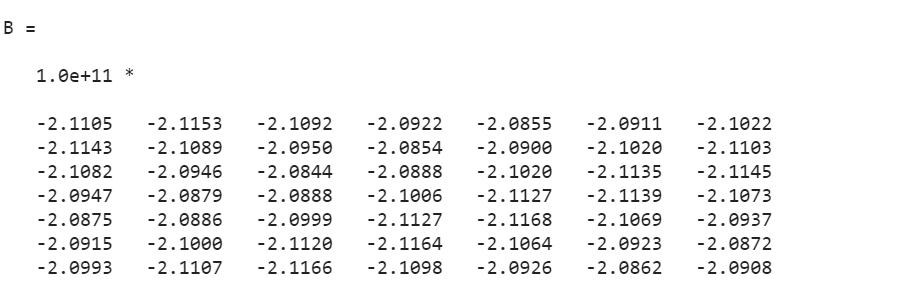
In this code, we create a square matrix of positive integers having dimension 7-by-7 using the magic() function. After that, we initialize a vector p that represents a polynomial . At the end, we use the polyvalm() function to evaluate the given polynomial p for matrix A and store the calculated results in matrix B.
p = [-9 7 3 5 1 -8];
B=polyvalm(p,A)
Example 2: How to Use the polyvalm() Function to Evaluate the Characteristic Polynomial of a Matrix in MATLAB?
The below-given example creates a matrix A of positive random integers having size 3-by-3 using the randi() function and also determines the characteristic polynomial p of the matrix A using the poly() function. After that, it implements the polyvalm() function to evaluate the characteristic polynomial p for matrix A and stores the results in matrix B.
p = poly(A)
B=polyvalm(p,A)
In the given output observe that the calculated matrix B is very close to 0 matrix. This follows the Cayley-Hamilton theorem which states that:
“If the polynomial is viewed as a matrix polynomial and evaluated at the matrix A itself, the result is the zero matrix”.

Conclusion
Evaluating a matrix polynomial is a complicated task when we perform it for higher-degree polynomials or a matrix having a size > 2. However, in the 20th century, we are blessed with high-performance computing tools like MATLAB that make our complicated tasks very easy by introducing a library having a variety of built-in functions. One such function is polyvalm() which evaluates a polynomial of a matrix in a very short amount of time. This tutorial has made a useful detailed discussion about matrix polynomials and their evaluation in MATLAB using some practical examples.
