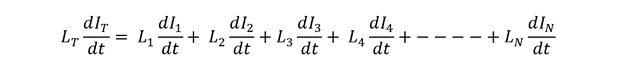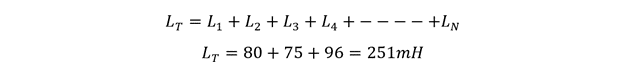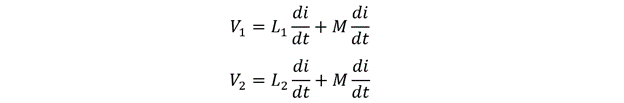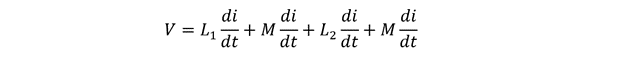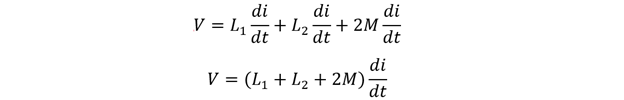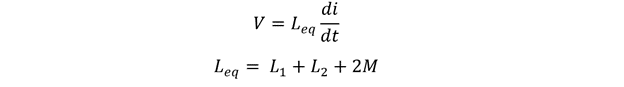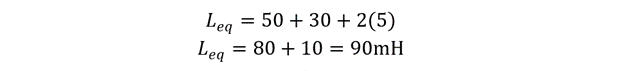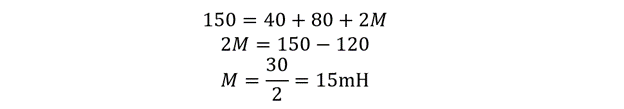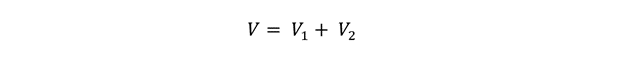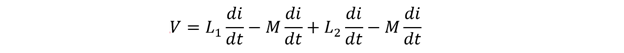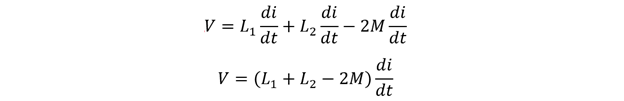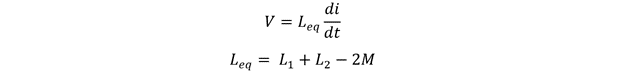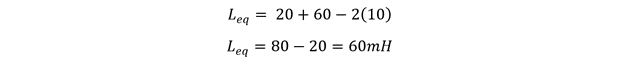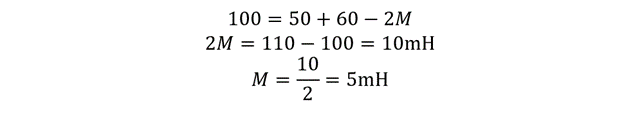Inductors in Series and Series Inductor Circuits

To ensure the proper functioning of any circuit, there are various electrical components and devices used like capacitors, resistors, and inductors. Each of these can be used for various purposes, inductors are normally used to prevent abnormal spikes in current by storing the energy in its magnetic field. To connect inductors, there are primarily two configurations, one in series and the other in parallel.

Inductor in Series

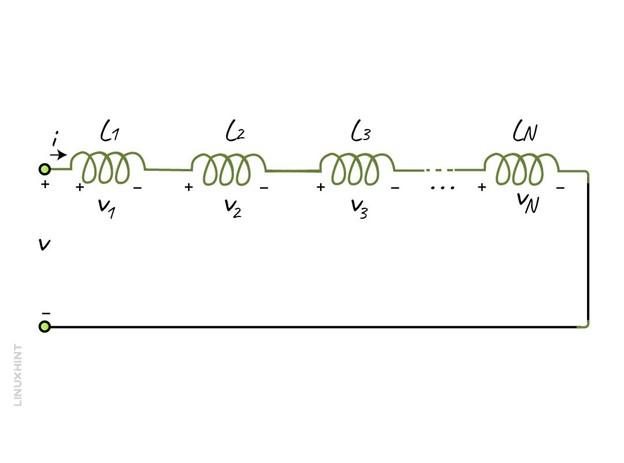
When the inductors are connected in a series connection, the equivalent inductance is relatively higher than the individual inductance of each inductor. Since in series configuration, the voltage across each of the inductors will be different whereas the current will be the same across each inductor to read further about how to connect inductors in series read this guide.

Here is a simple circuit in which inductors are connected in series:

As mentioned above, the current is the same in the series, so we can say that:

Now, for calculating the voltage across each inductor, we can use the following equation:

So, to calculate the total voltage, sum up the voltage across each inductor:

Now, the equation for calculating the voltage can be written as:

Now we can further simplify the equation to find the formula for calculating the equivalent inductance:

So now the equation for the equivalent formula can be written as:

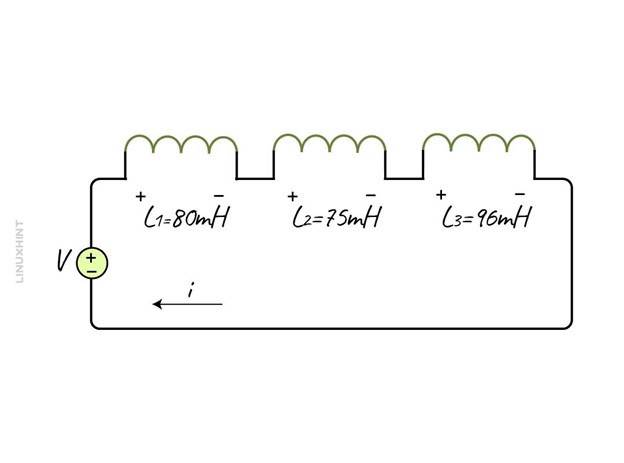
Example: Calculating the Equivalent Inductance of Series Inductors

Consider three inductors connected on a series combination having an inductance of 80mH, 75mH, and 96 mH. Find the equivalent inductance of the inductors connected in series.

Finding the equivalent inductance using:

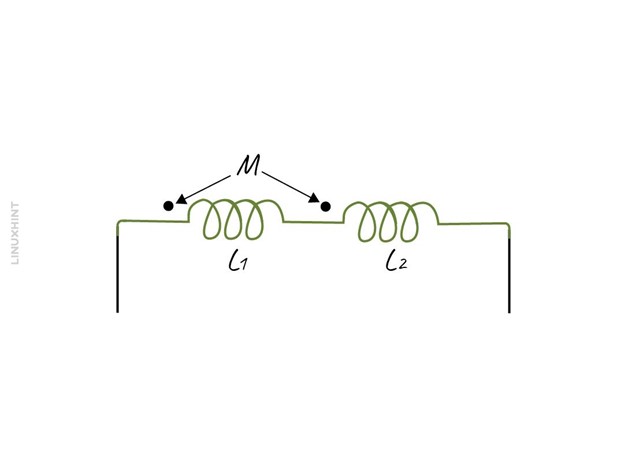
Magnetic Coupled Inductors in Series

When the magnetic field of one inductor links with the magnetic field of the other inductor in a series combination, this is often referred to as magnetic coupling or mutual inductance between the two inductors. So, in that case, mutual inductance is to be considered while calculating the equivalent inductance of the circuit. Further, the mutually coupled inductors are classified into two configurations and those are:

Cumulatively coupled or series Aiding inductors
Differentially coupled or series opposing inductors

Cumulatively Coupled or Series Aiding Inductors

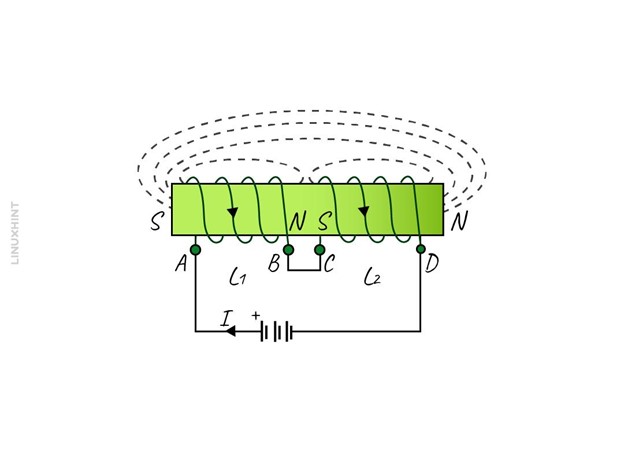
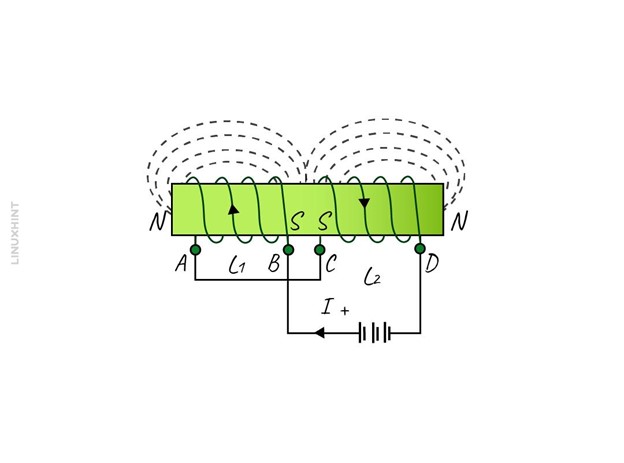
When the direction of the current following through both the mutually coupled series combination inductors is the same, then it means that there are aiding inductors:

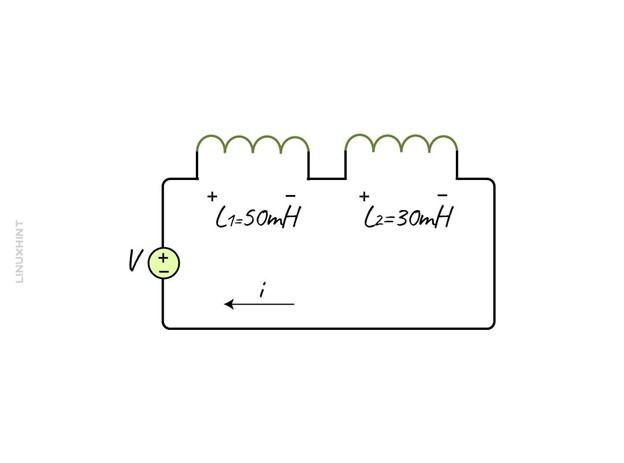
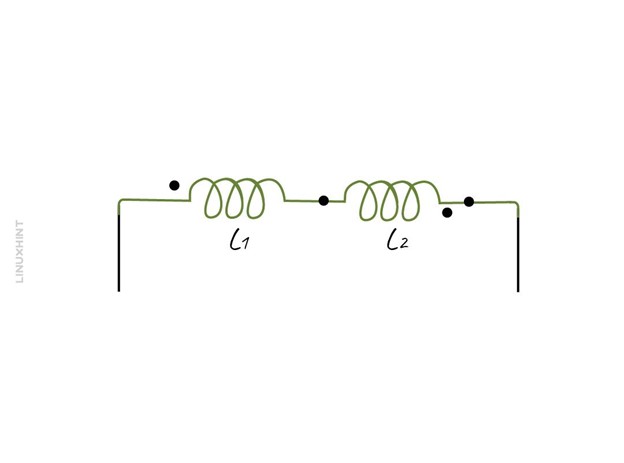
Usually, to represent this configuration a dot convention is used and for aiding configuration, the dots are on the same sides of the inductors in series:

Here, M is the mutual inductance between the two coils, so to calculate the equivalent inductance of a series inductor combination it is necessary to consider mutual inductance. The EMF of the inductors can be calculated as:

Now the total EMF for the coil will be:

Putting the values for EMF for each coil we get:

Now further simplifying the equation, we get the following:

So now the equation for equivalent inductance will be:

Here, 2M is the mutual inductance between the coils in the circuit, which is the effect that both coils have on each other.

Example 1: Calculating the Equivalent Inductance of Series-Aided Inductors

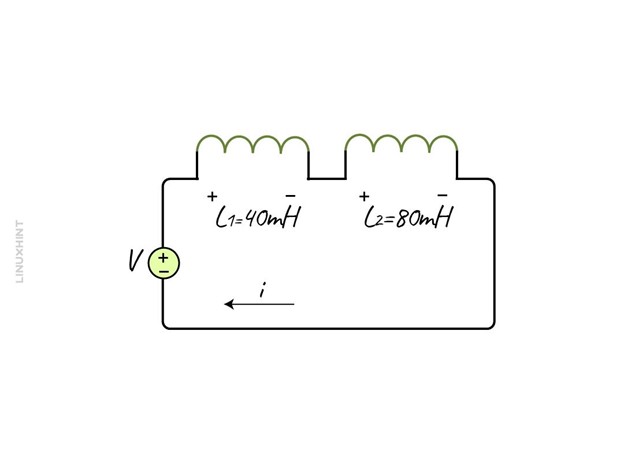
Two inductors having an inductance of 50mH and 30 mH are connected in series, the mutual inductance between the two is 5mH when the current direction is the same for both coils.

To calculate the equivalent inductance, below is the equation:

Now placing the values, we get:

Example 2: Calculating the mutual inductance of Series-Aided Inductors

If the inductance of two coils connected in a series configuration is 40mH and 80mH and the equivalent inductance is 150mH. The value of mutual inductance is unknown, so if the series inductors are aiding (current in the same direction) then:

Now placing the values in the above equation, we get:

The mutual inductance between the two coils is 15mH.

Differentially Coupled or Series Opposing Inductors

When the current passing through the coil is the same but the direction of current in both coils is opposite, then the inductors are said to be opposing:

Usually, to represent this configuration a dot convention is used and for the opposing configuration, the dots are on the opposing sides of the inductors in series:

Now the total EMF for the coil will be:

Putting the values for EMF for each coil we get:

Now further simplifying the equation, we get the following:

So now the equation for equivalent inductance will be:

Here, 2M is the mutual inductance between the coils in the circuit and is the effect that coils have on each other.

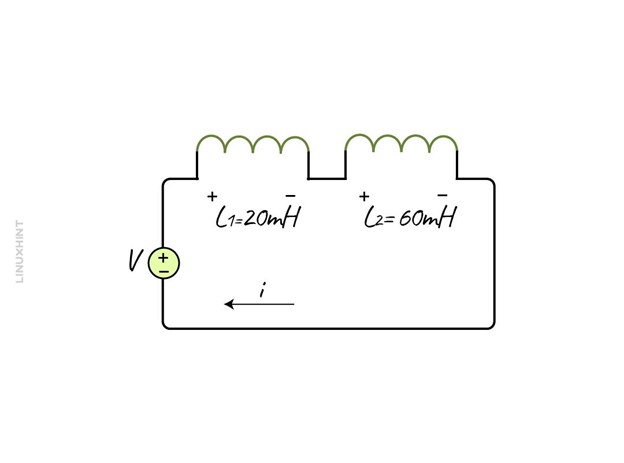
Example 1: Calculating the Equivalent Inductance of Series-Opposed Inductors

The two inductors connected in series have an inductance of 20mH and 60mH having a mutual inductance of 10mH. To calculate the equivalent inductance, below is the equation:

Now placing the values for the inductance and mutual inductance

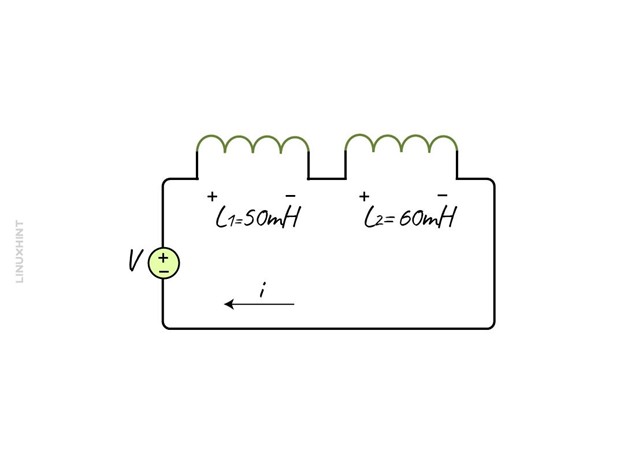
Example 2: Calculating the Mutual Inductance of Series-Opposed Inductors

If the inductance of two coils connected in a series configuration is 50mH and 60mH and the equivalent inductance is 100mH. The value of mutual inductance is unknown, so if the series inductors are opposing then:

Now placing the values in the above equation, we get:

The mutual inductance between the two coils is 5mH.

Conclusion

In series combination, the inductors have the equivalent inductance higher than the individual inductance in the circuit. Moreover, the series configuration is further divided into two configurations, one is when both have the same direction of current and the other is when the direction of current is opposite. To calculate the equivalent inductance in series, just sum all the individual inductance.

For mutually coupled indicators, sum the individual inductance as well as either sum or subtract the double of mutual inductance, depending on the direction of the current.