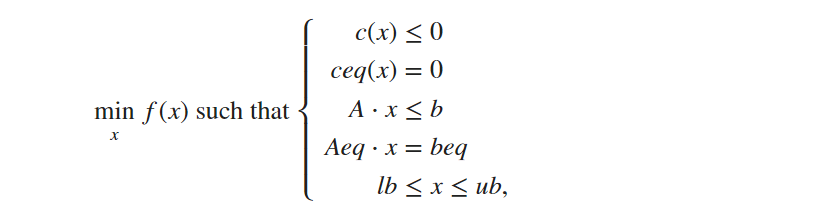Solving a nonlinear optimization problem is a complicated task that requires complex calculations and it is time-consuming. However, we are thankful to MATLAB which provides us with a built-in function fmincon() to solve such nonlinear optimization problems.
In this article, we are going to discuss:
- What is a Nonlinear Optimization Problem
- How to Perform Nonlinear Optimization in MATLAB Using the fmincon() Function
- Examples
- Conclusion
What is a Nonlinear Optimization Problem
In general, an optimization problem is the process of selecting n decision variables from the given feasible region to optimize an objective function of decision variables. This problem is called a non-linear programming problem if the objective function is nonlinear subject to some linear or nonlinear constraints. This type of problem has the following mathematical form.
Find the minimum of a given problem specified by:
Where,
- f(x) represents an objective function.
- b and beq represent vectors.
- A and Aeq represent matrices.
- c(x) and ceq(x) represent functions.
- lb, x, and ub can be vectors or matrices.
The functions f(x), c(x), or ceq(x) can be non-linear.
How to Perform Nonlinear Optimization in MATLAB Using the fmincon() Function
MATLAB allows us to calculate the minimum of a nonlinear optimization problem using the fmincon() function. This function accepts some mandatory and some optional inputs and returns the calculated minimum of the given nonlinear optimization problem.
Syntax
The fmincon() function can be implemented through the following syntaxes:
x = fmincon(fun,x0,A,b,Aeq,beq)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
x = fmincon(problem)
[x,fval] = fmincon(___)
[x,fval,exitflag,output] = fmincon(___)
[x,fval,exitflag,output,lambda,grad,hessian] = fmincon(___)
Here,
The function x = fmincon(fun,x0,A,b) is responsible for calculating the value of minimizer x of the objective function fun subject to the linear inequality constraints having the form . This function starts calculation from the initial guess x0 where x0 can be a scalar or an array.
The function x = fmincon(fun,x0,A,b,Aeq,beq) is responsible for calculating the value of the minimizer x of the objective function fun starting from the initial guess x0 subject to the linear inequality constraints or equality constraints eq. If there are no inequality constraints, we can set A =[] and b=[] or Aeq =[] and beq=[], if no equality constraints exist here.
The function x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub) is responsible for calculating the value of the minimizer x of the objective function fun starting from the initial guess x0 subject to the linear equality constraints or inequality constraints defining the set of upper and lower bounds such that . Set lb(i) = -inf, whenever x(i) is unbounded below or ub(i) = inf whenever x(i) is unbounded above.
The function x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon) is responsible for calculating the value of the minimizer x of the objective function fun subject to the non-linear equality constraints or inequality constraints defined by the user-defined function nonlcon. This function starts calculations from the initial guess x0. The variables A,b, Aeq, and beq represent linear inequality and equality constraints that can be set equal to [] if they do not exist. The lower bound lb and upper bound ub are used to define lower and upper bounds.
The function x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options) is responsible for calculating the value of the minimizer x of the objective function fun subject to the linear and nonlinear equality or inequality constraints starting from the initial guess x0 by specifying the optimization options.
The function x = fmincon(problem) is responsible for calculating the value of the minimizer x of the function described by the problem structure.
The function [x,fval] = fmincon(___) is responsible for calculating the value of the minimum x of the objective function. Also, it determines the functional value of the given objective function at the calculated solution x using any previous syntax.
The function [x,fval,exitflag,output] = fmincon(___) is responsible for determining the minimum x of the function, functional value fval of the objective function, the exit conditions exitflag of the fmincon, and the output structure that describes the optimization process.
The function [x,fval,exitflag,output,lambda,grad,hessian] = fmincon(___) is responsible for determining the parameters:
- x: represents the minimum value of the given objective function.
- fval: represents the objective function value at solution x.
- exitflag: represents the exit conditions of the function fmincon.
- output: represents the structure that provides information about the optimization process.
- lambda: represents the structure having fields that contain the Lagrange multiples at the solution x.
- grad: represents the gradient of the function at solution x.
- hessian: represents the hessian of the function at the solution x.
Examples
Consider some examples to practically implement the fmincon() function for solving nonlinear optimization problems in MATLAB.
Example 1: How to Perform Nonlinear Optimization Using Linear Inequality Constraints
This MATLAB code uses the x = fmincon(fun,x0,A,b) function to calculate the minimum of the objective function fun having the mathematical form subject to linear inequality constraint . This inequality constraint has the form A =[2,5] and b=10 in MATLAB. This code selects x0=[-1,1] as an initial guess
x0 = [-1,1];
A = [2,5];
b = 10;
x = fmincon(fun,x0,A,b)
Example 2: How to Perform Nonlinear Optimization Using Linear Equality and Inequality Constraints
The given example implements the function x = fmincon(fun,x0,A,b,Aeq,beq) to calculate the minimum of the objective function fun having the mathematical form subject to linear inequality constraint and equality constraint . The inequality constraint has the form A =[2,5] and b=10 while the equality constraint has the form A_eq=[1,1] and b_eq=2 in MATLAB. This code selects x0=[-1,1] as an initial guess
x0 = [-1,1];
A = [2,5];
b = 10;
A_eq = [1,1];
b_eq = 2;
x = fmincon(fun,x0,A,b,A_eq,b_eq)
Example 3: How to Perform Nonlinear Optimization Using Nonlinear Constraints
In the given example, we use the x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon) function to calculate the minimum of the objective function fun having the mathematical form subjects to the non-linear inequality constraint . This inequality constraint is defined in the user-defined function @unitdisk. The expression ceq=[] represents, there is no nonlinear equality constraint. The given block of code describes the function @unitdisk defined in the script file named @unitdisk.
c = x(1)^2 + x(2)^2;
ceq = [];
Given below is the main program that uses the initial guess x0=[-1,1] to calculate the minimum of the given objective function subject to the non-linear constraints. Here, we assign the value of the user-defined function @unitdisk to the nonlcon variable. As there is no set of linear inequality and equality constraints we set these constraints equal to []. Also, there are no upper and lower bounds so we set them equal to [].
nonlcon = @unitdisk;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
x0 = [-1,1];
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
Example 4: How to Perform Nonlinear Optimization Using Linear and Nonlinear Equality and Inequality Constraints
The given example implements the function x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon) function to calculate the minimum of the objective function fun having the mathematical form subject to the linear inequality constraint and equality constraint , and non-linear inequality constraints . This non-linear inequality constraint is defined in the user-defined function @unitdisk. The expression ceq=[] represents, there is no nonlinear equality constraint. The given block of code describes the definition of the function @unitdisk in the script file named @unitdisk.
c = x(1)^2 + x(2)^2;
ceq = [];
Given below is the main program that uses the initial guess x0=[-1,1] to calculate the minimum of the given objective function subject to the linear and non-linear constraints. Here, the linear inequality constraint has the form A =[2,5] and b=10 while the equality constraint has the form A_eq=[1,1] and b_eq=2 in MATLAB. We assign the value of the user-defined function @unitdisk to the nonlcon variable. As there are no upper and lower bounds we set them equal to [].
nonlcon = @unitdisk;
A = [2,5];
b = 10;
A_eq = [1,1];
b_eq = 2;
x0 = [-1,1];
lb =[];
ub =[];
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
Example 5: How to Perform Nonlinear Optimization by Minimizing With Bound Constraints
In this MATLAB code, we use the x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub) function to calculate the minimum of the objective function fun having the mathematical form subject to linear inequality constraint and equality constraint . Here, the linear inequality constraint has the form A =[2,5] and b=10 while the equality constraint has the form A_eq=[1,1] and b_eq=2 in MATLAB. This code selects the lower bound lb=[0,0] and upper bound ub=[1,2].
lb = [0,0];
ub = [1,2];
x0 = (lb + ub)/2;
A = [2,5];
b = 10;
A_eq = [1,1];
b_eq = 2;
x = fmincon(fun,x0,A,b,A_eq,b_eq,lb,ub)
Example 6: How to Perform Nonlinear Optimization to Obtain Objective Function Value
The given example uses the [x,fval] = fmincon(___) function to calculate the minimum of the objective function fun having the mathematical form . After that, it determines the objective function value at the determined solution x. This code selects x0=[-1,1] as an initial guess. As there is no set of equality and inequality constraints, so we set them equal to [].
A = [];
b = [];
Aeq = [];
beq = [];
x0 = [-1,1];
[x,fval] = fmincon(fun,x0,A,b,Aeq,beq)
Example 7: How to Perform Nonlinear Optimization Examining Solutions Using Extra Outputs
This example works as Example 3 having the difference that it implements the [x,fval,exitflag,output] = fmincon(___) function for calculating and displaying extra outputs such as fval, exitflag, and output.
nonlcon = @unitdisk;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
x0 = [-1,1];
[x,fval,exitflag,output] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
Example 8: How to Perform Nonlinear Optimization Displaying All Outputs
The given MATLAB code works in the same way as Example 3. But it implements [x,fval,exitflag,output,lambda,grad,hessian] = fmincon(___) to calculate and display all possible outputs such as fval, exitflag, output, lambda, grad, and hassian.
nonlcon = @unitdisk;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
x0 = [-1,1];
[x,fval,exitflag,output,lambda,grad,hessian] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
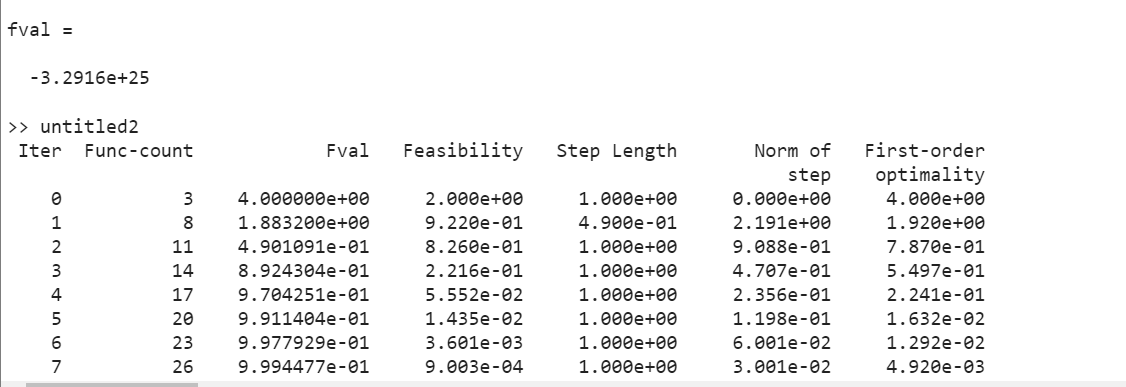
Example 09: How to Perform Nonlinear Optimization Using Non-Default Options
This is another technique for solving the non-linear optimization problem discussed in Example 3. This technique uses the x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options) function to implement nondefault options such as iter for displaying occurred iterations and sqp algorithm , to solve the given problem, which is faster and more accurate than the default algorithm interior point.
nonlcon = @unitdisk;
options = optimoptions('fmincon','Display','iter','Algorithm','sqp');
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
x0 = [-1,1];
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
Example 10: How to Perform Nonlinear Optimization Using Problem Structure
In this example, we use the nondefault option for solving the non-linear optimization problem as discussed in Example 3 using the problem structure instead of separate arguments.
problem.options = options;
problem.solver = 'fmincon';
problem.objective= @(x)(x(2)-x(1))^2 + 1-x(1)^2;
problem.x0 = [-1,1];
problem.nonlcon = @unitdisk;
x = fmincon(problem)
Conclusion
Solving nonlinear optimization problems is a widely used task in mathematics and engineering for finding maxima, minima, or stationary points of a function. This is a complicated task that might require a large number of iterations or calculations. However, we can easily and efficiently solve this problem using the fmincon() function in MATLAB. This guide has presented all possible ways for implementing the fmincon() function in MATLAB.