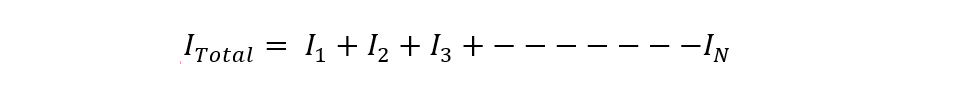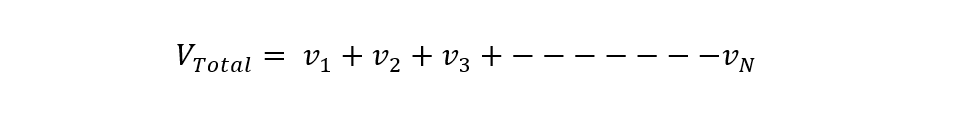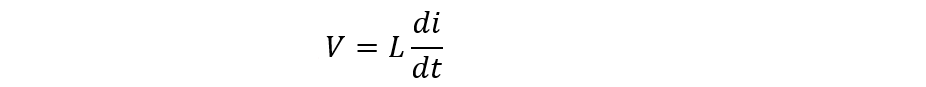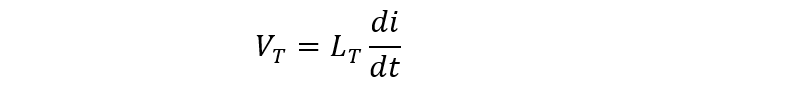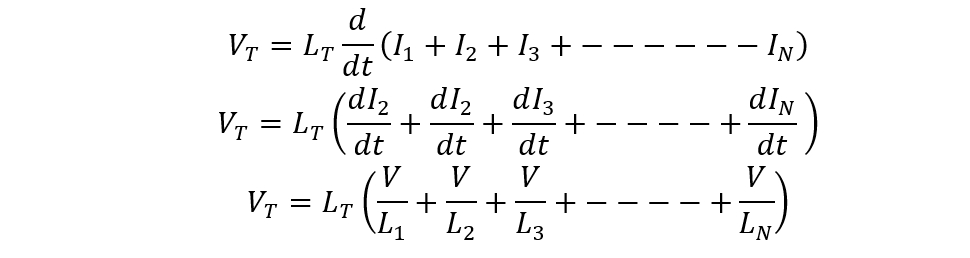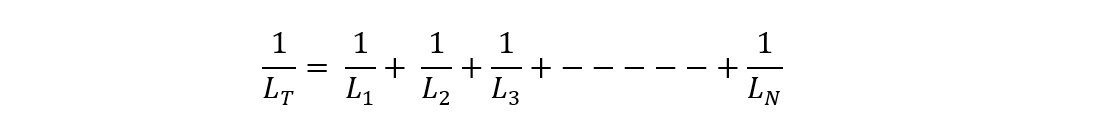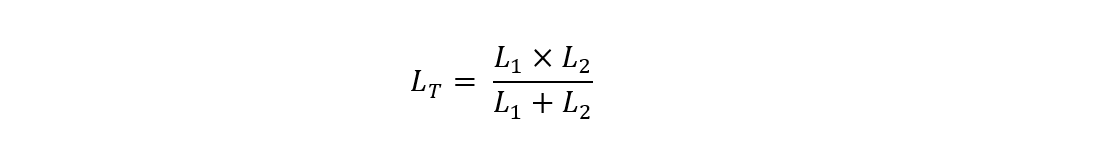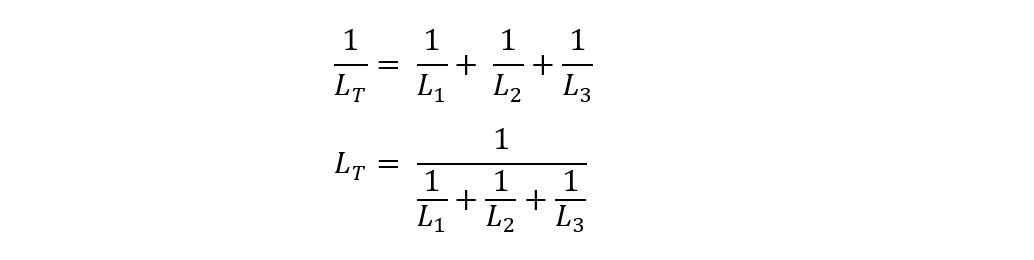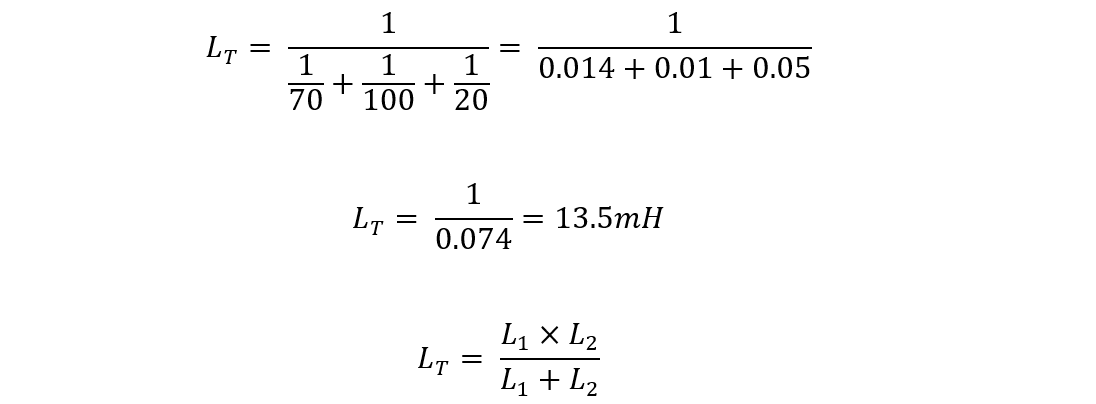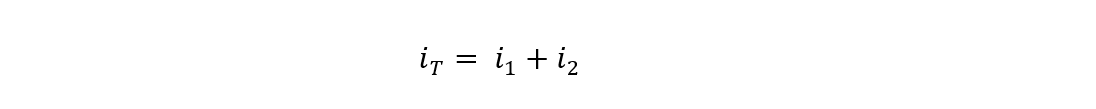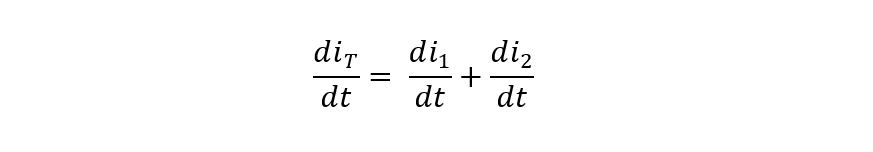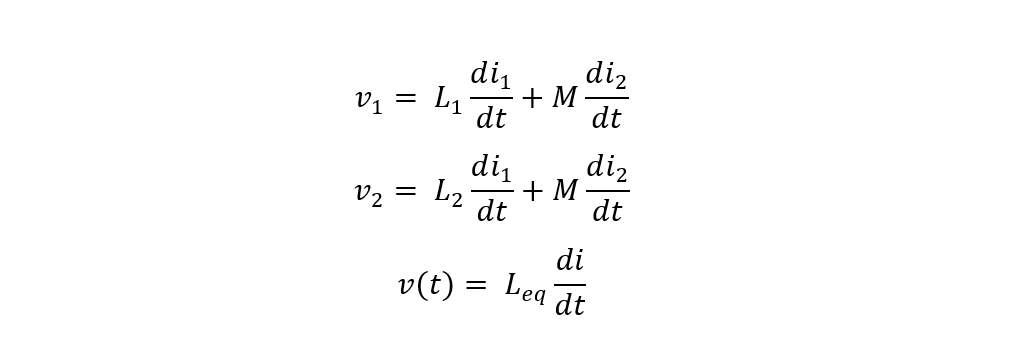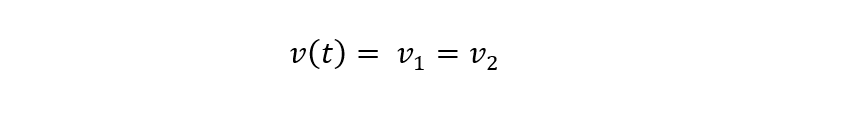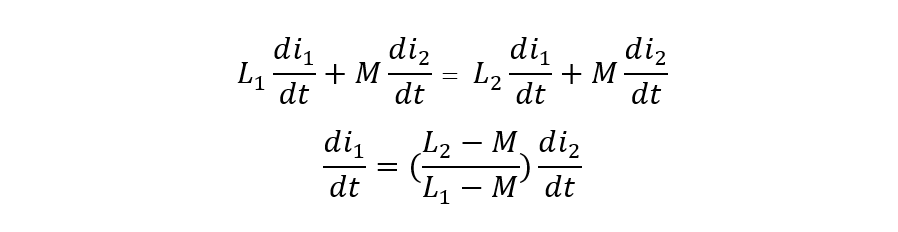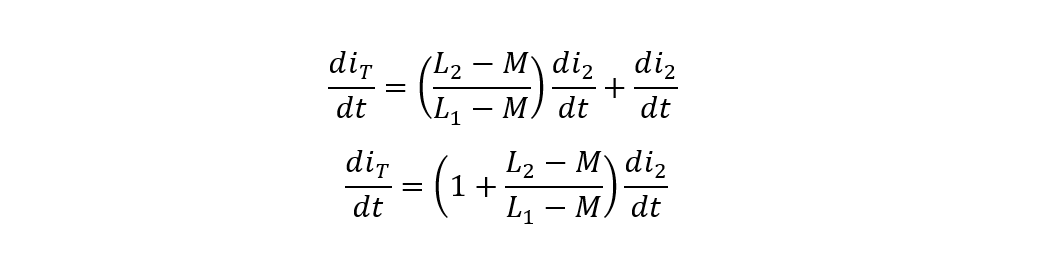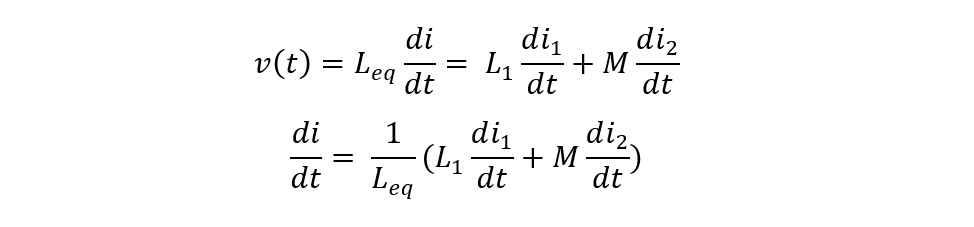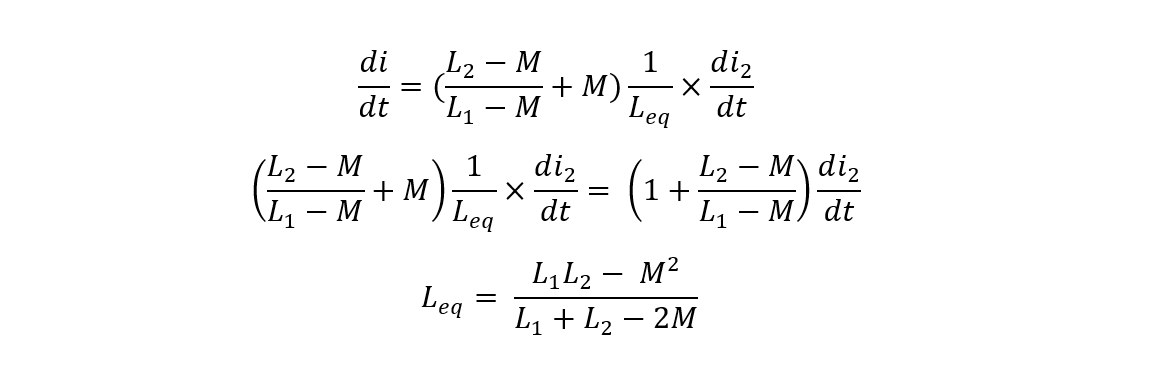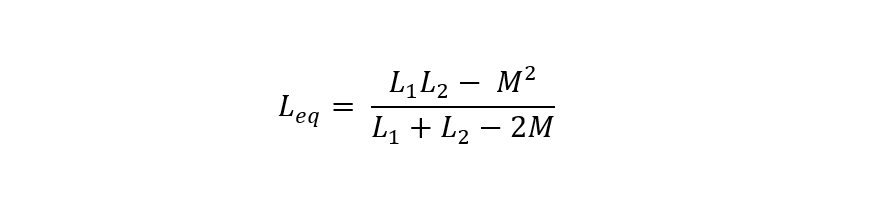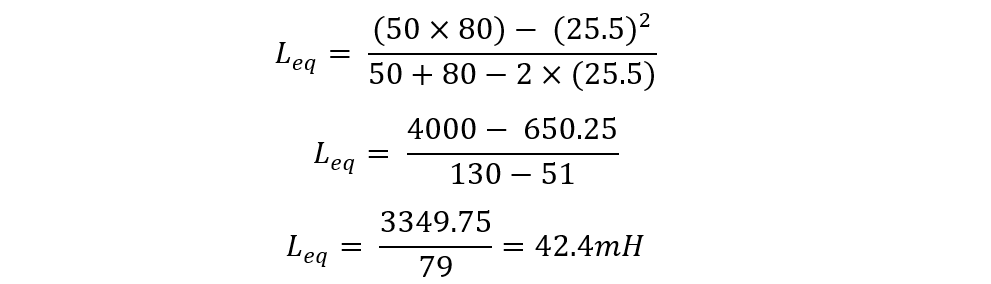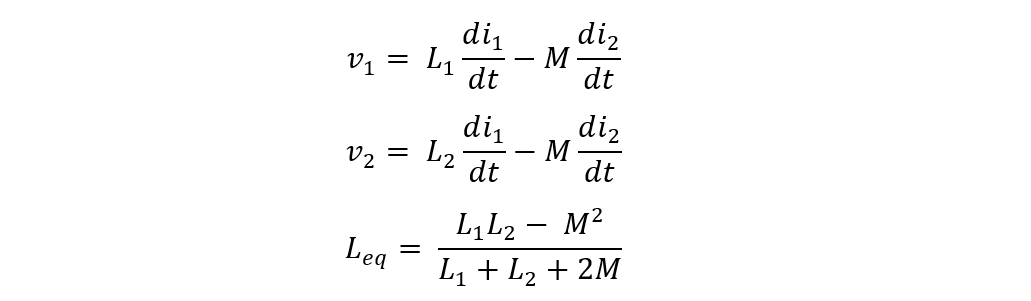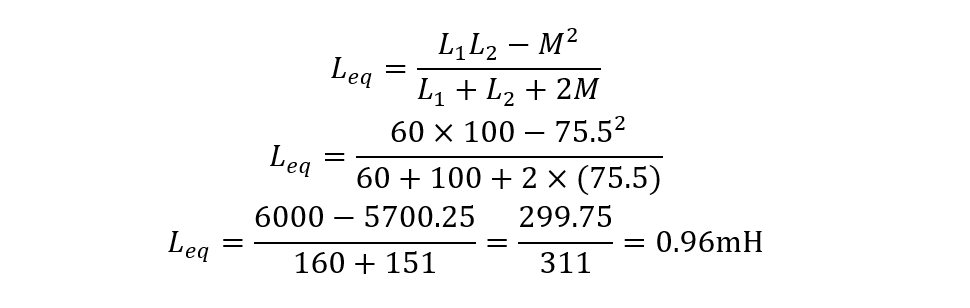Outline:
Inductors in Parallel
The combination of inductors with other circuit components solemnly depends on the working of the circuit, and there are two ways to connect inductors in a circuit, one is in a series configuration and the other is in a parallel configuration. If you need more detailed information about connecting inductors in series and parallel, then read this guide.
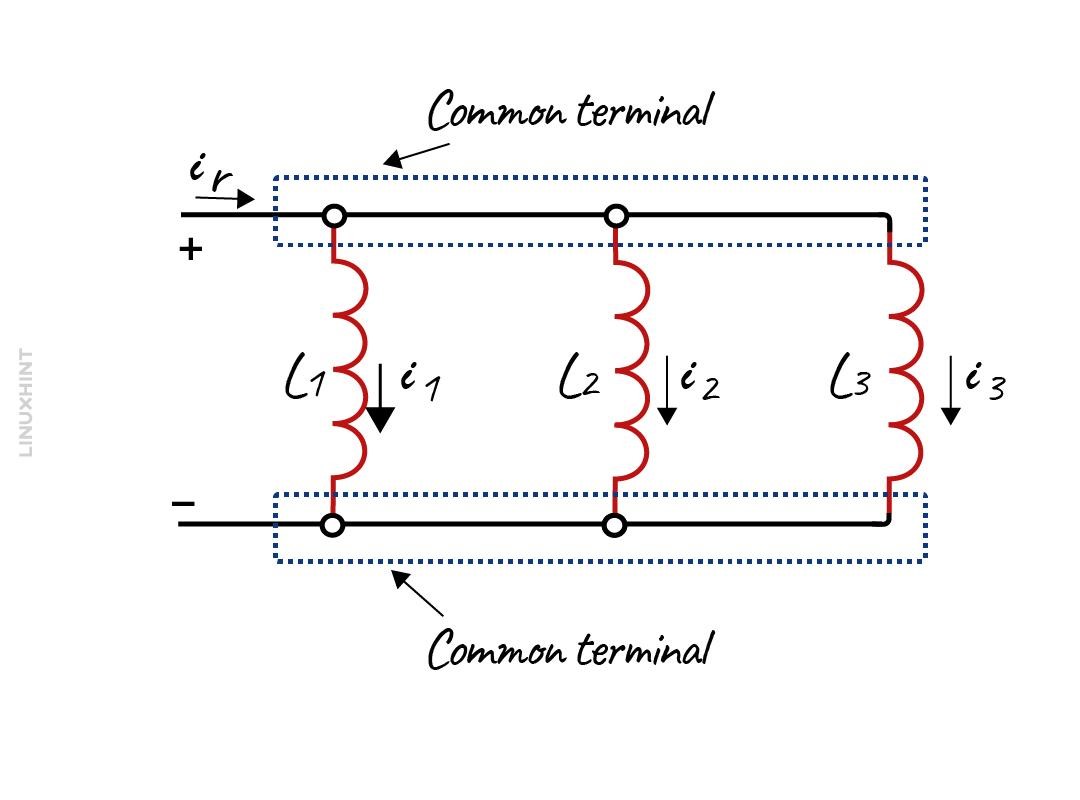
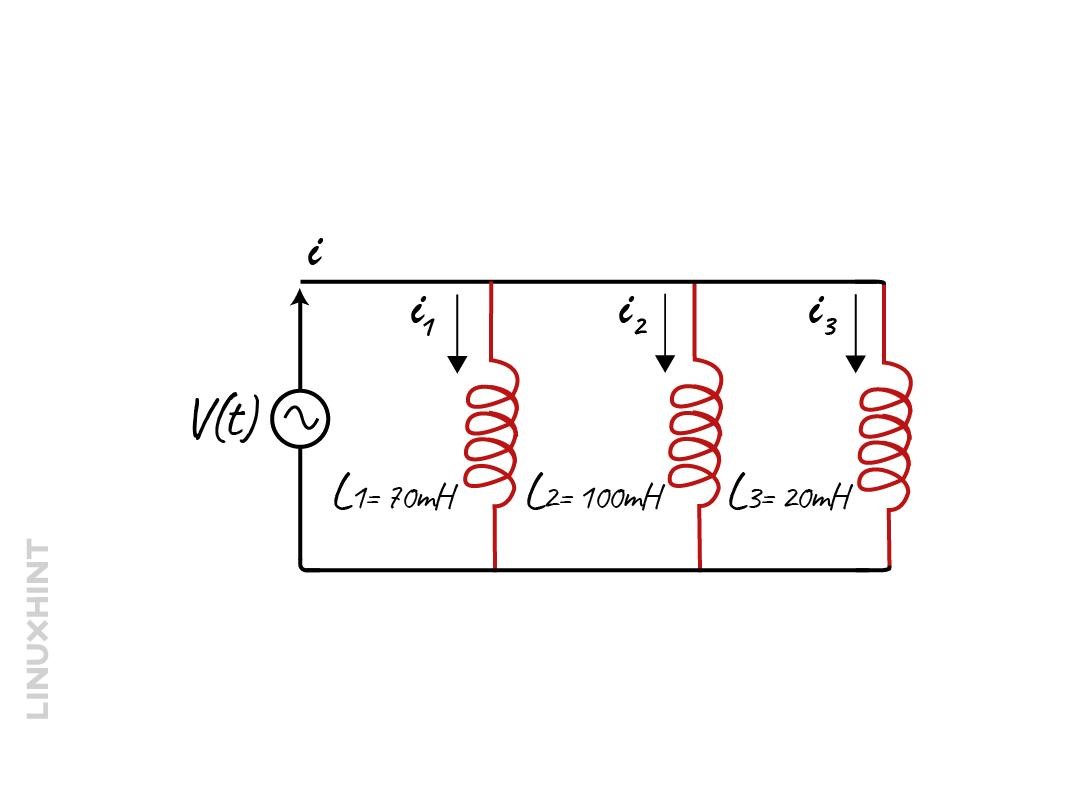
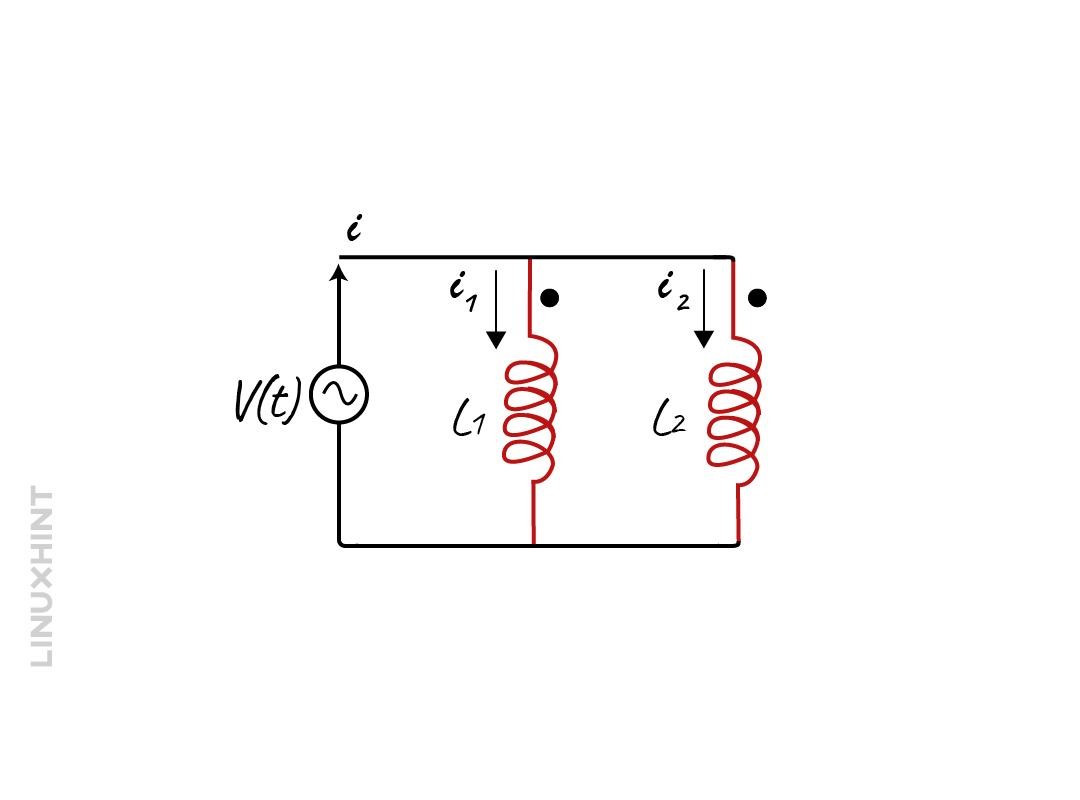
In parallel connection of inductors, the overall equivalent inductance is decreased, and the voltage will be the same across each of the inductors, below is the configuration of parallel connection of inductors:
This is a simple configuration of inductors, so to calculate the equivalent inductance below is the derivation in case the inductors are not magnetically coupled using the above-given inductors configuration:
To calculate the total current, sum up the individual currents of the inductors:
Furthermore, to calculate the total voltage, sum up the individual voltage across each inductor:
Now as we know in the case of self-inductance the voltage drop will be:
So, the total voltage will be:
Now, using the same formula for total inductance as for the total voltage:
Now, from the above equation, it can be seen that the in parallel configuration equivalent inductance is the sum of all the reciprocals of individual inductance:
Now for simplicity, the above formula can be simplified as the product of all the inductance of inductors divided by the sum of all the inductance of the inductors in the case of two parallel inductors:
Example: Calculating the Equivalent Inductance of Parallel Inductors
Consider three inductors connected in parallel having the individual inductance of 70mH, 100mH, and 20mH. Find their equivalent inductance.
To find the equivalent inductance in parallel below is equation:
Now for total inductance, placing the values:
Mutually Coupled Parallel Inductors
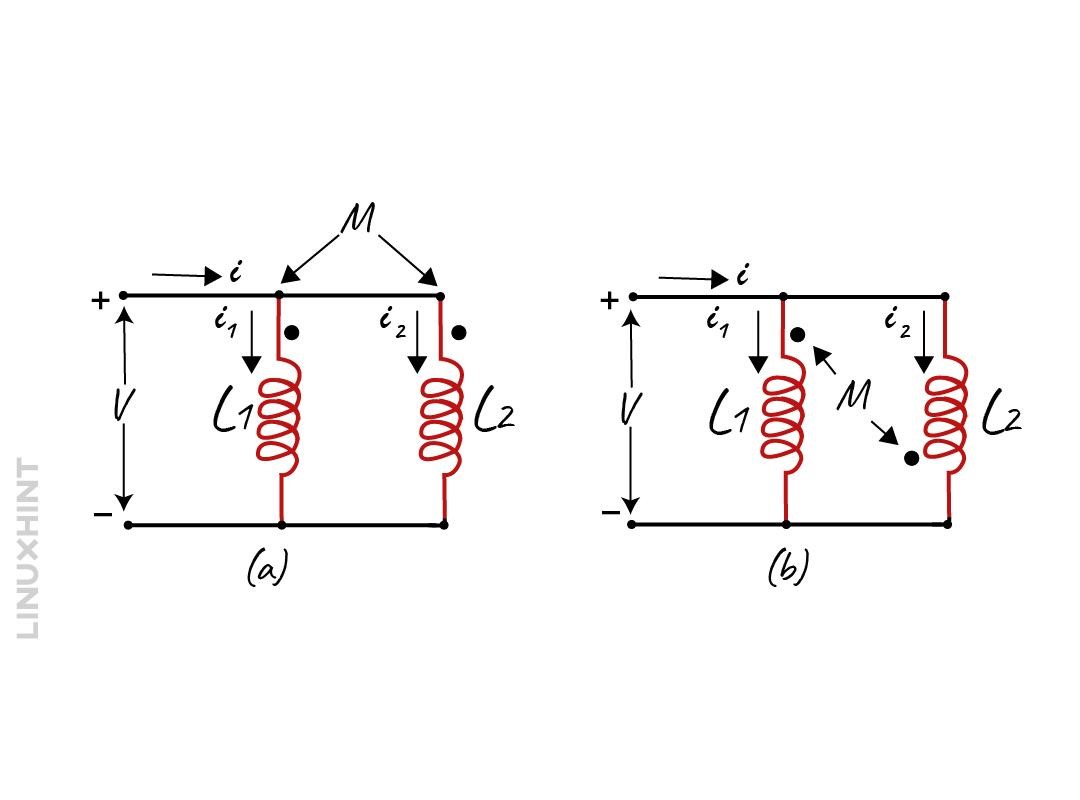
When the inductors are magnetically coupled, the inductance can vary based on the principle of mutual inductance so that the equation for the equivalent inductance is to be altered. However, there are further two types of configurations in the case of magnetic coupling, one is aiding coils and the other is opposing coils.
To distinguish between the opposing and aiding coils, the dot convention is normally used if the dots are on opposite sides, then it means that they are opposing and vice versa.
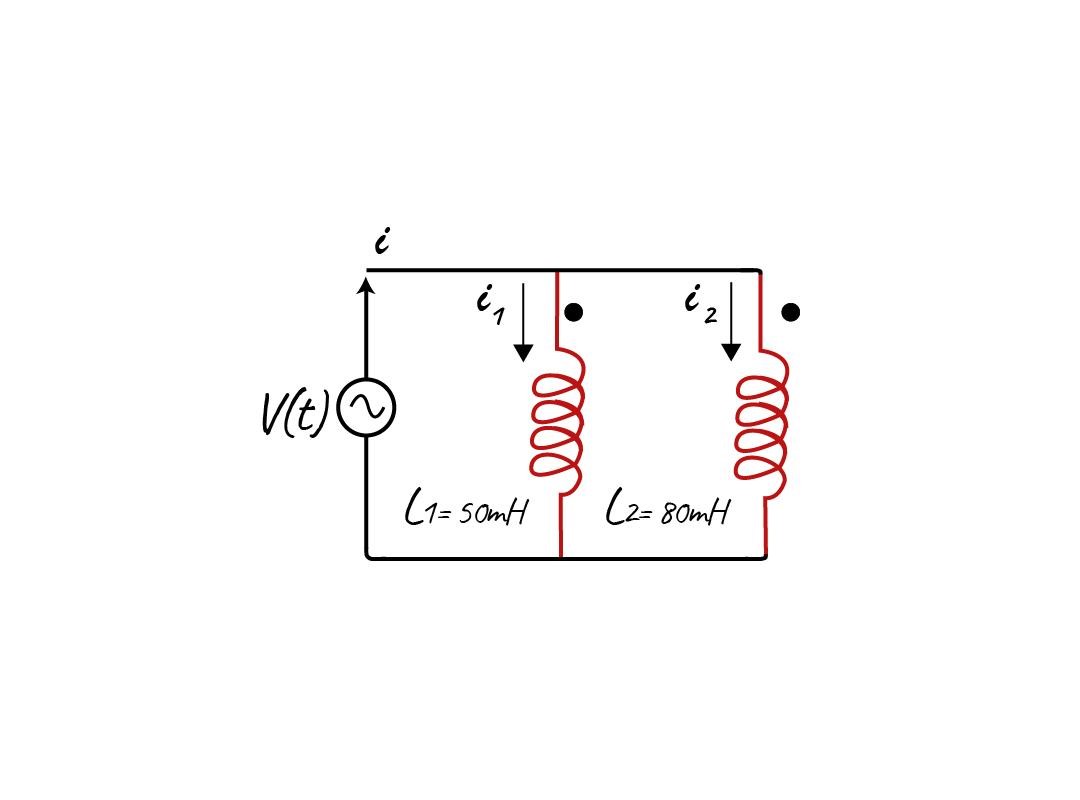
Parallel Aiding Inductors
When both inductors have the same polarity, they are referred to as the aiding inductors, as a result, the equivalent inductance will be more as compared to the inductance of the coils with no magnetic coupling:
As from the above circuit, the total current will be the sum of the individual branch currents of the inductors:
Since the current varies, taking differentiation for the above current equation:
Now the voltage across the inductor L1 can be written as:
Since the inductors are in parallel, the voltage will be the same across both, so in that case, it can be assumed that:
Now, comparing both equations for voltages of inductors:
Now substituting the value for the rate of change of current through the first inductor:
Now equating all the equations, we get:
Now placing the values of di/dt we get:
The 2M in the above equation is the effect of both coils on each other and if both coils have the same inductance, it means that they are perfectly coupled, so in that case the inductance will be L. Moreover, if the mutual inductance is zero among the coils, then the inductance will be divided by 2.
Example: Calculating the Equivalent Inductance of Parallel-Aided Inductors
Consider two parallel-aided inductors having the inductance of 50mH and 80mH, their mutual inductance is 25.5mH. Find the equivalent inductance of the inductor in parallel.
To calculate the equivalent inductance, use the below-given equation:
Now placing the respective values:
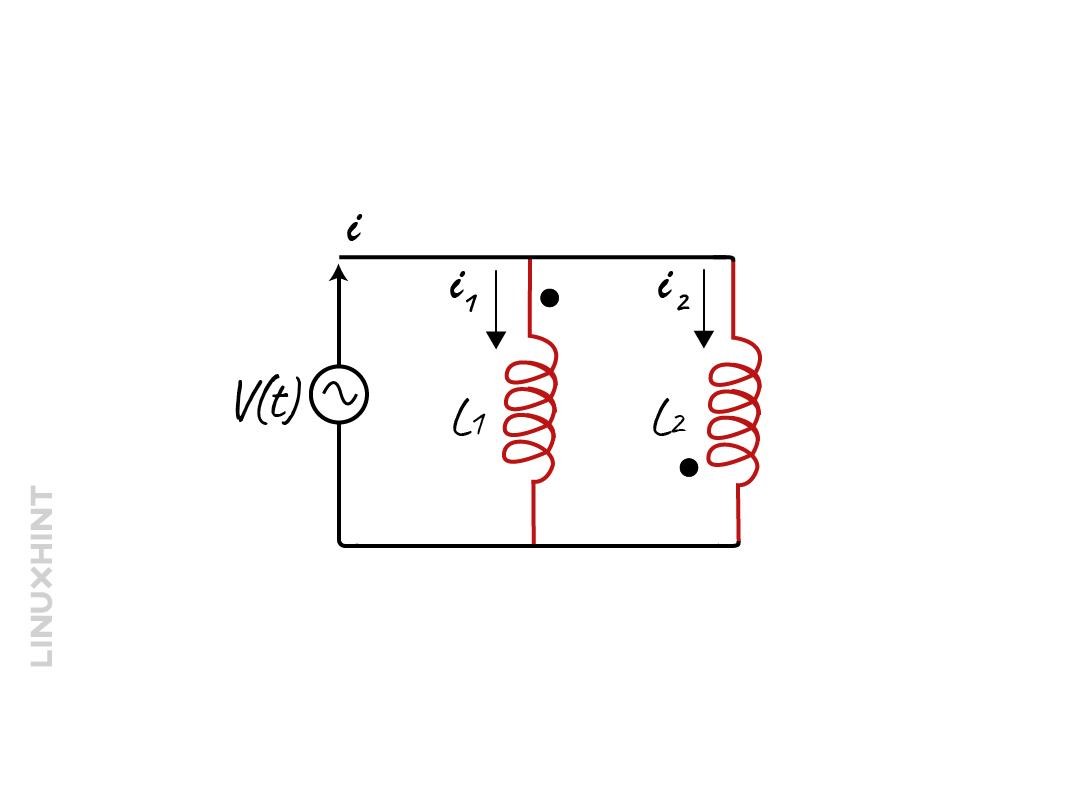
Parallel Opposing Inductors
When the direction of the magnetic flux is opposite to that of the flux produced, then the inductors are said to be opposing and, in this case, the equivalent inductance is less than the individual inductance of the inductors.
The process for derivation of the formula for finding the equivalent inductance of the parallel opposing inductors is similar, and the only difference is the induced voltage so from the equation of voltage from the previous derivation:
Example: Calculating the Equivalent Inductance of Parallel-Opposed Inductors
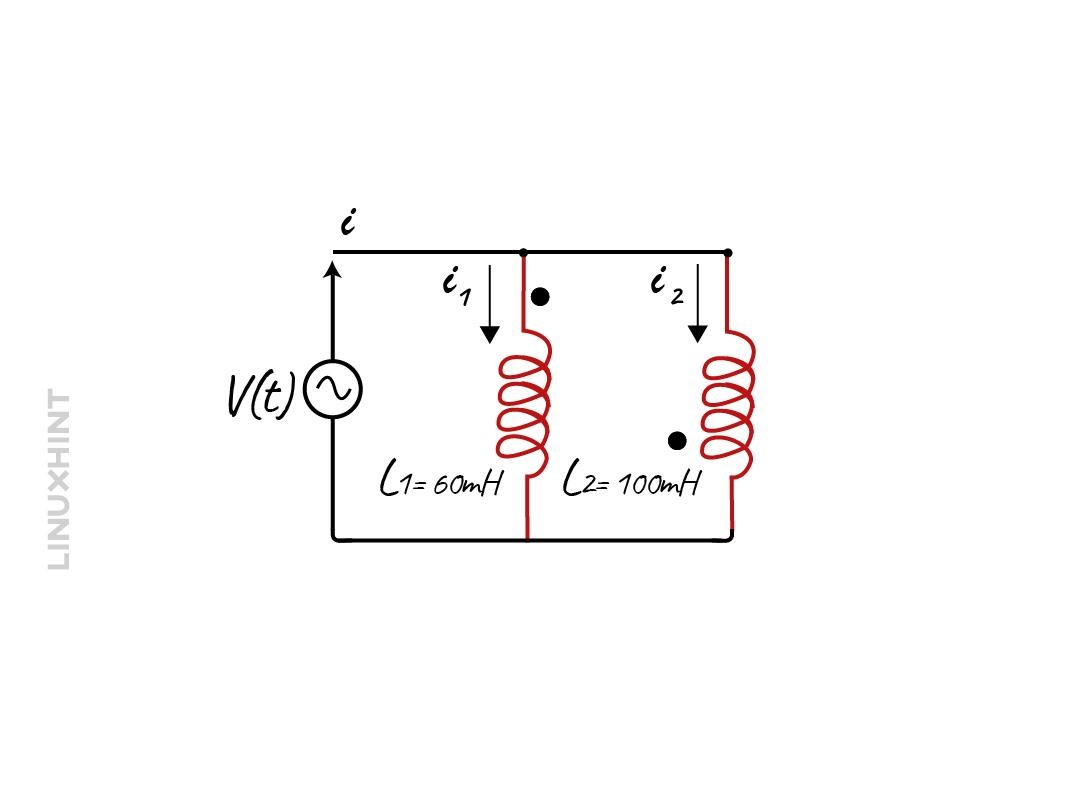
Consider two parallel-opposed inductors having the inductance of 60mH and 100mH, their mutual inductance is 75.5mH. Find the equivalent inductance of the parallel opposed inductors.
To calculate the equivalent inductance, use the below-given equation:
Conclusion
The Inductor configuration for connecting them in circuits depends on the desired output of a respective circuit, normally there are two configurations one is series and the other is parallel. In a parallel configuration, there are further two configurations, one is when there is no magnetic coupling between the two inductors and the other is when both are magnetically coupled with each other either opposing or aiding