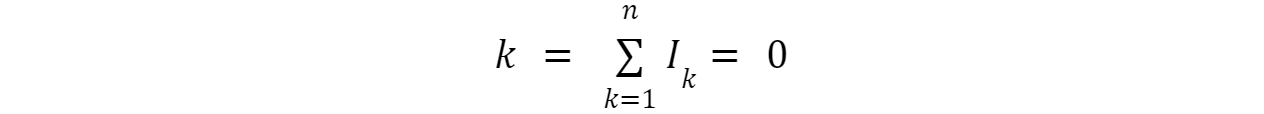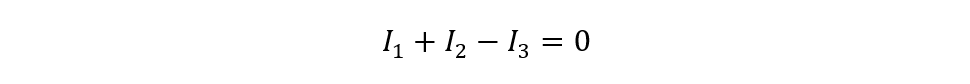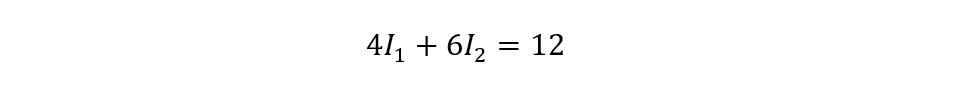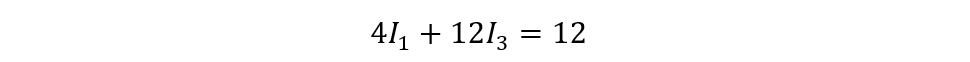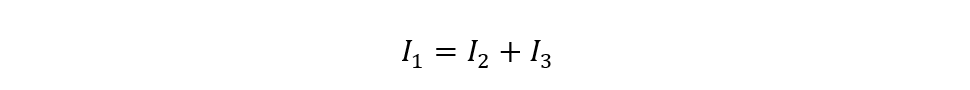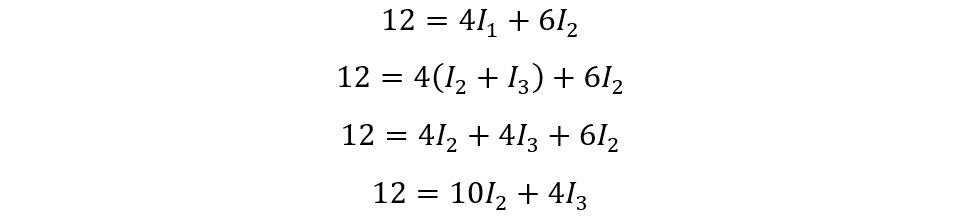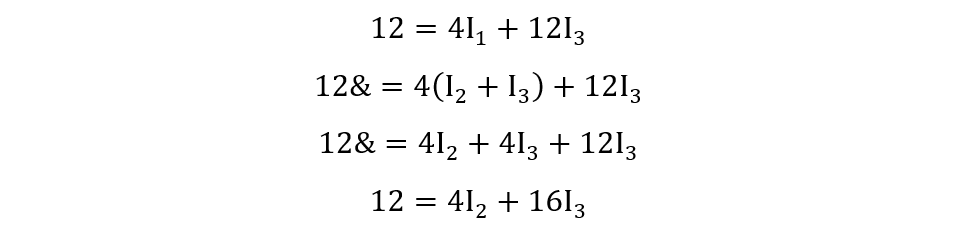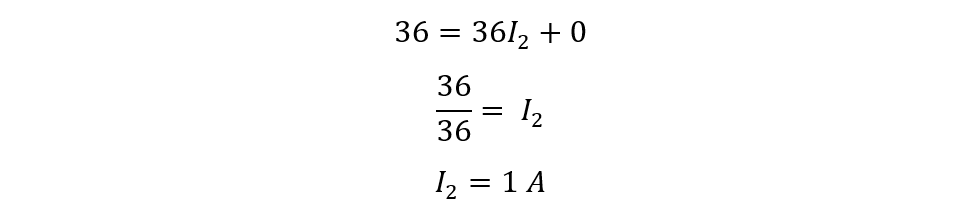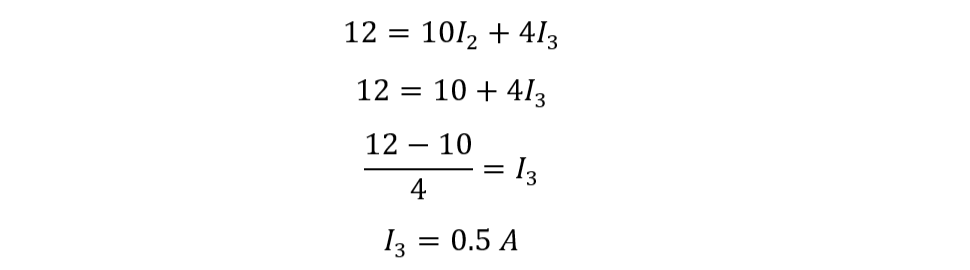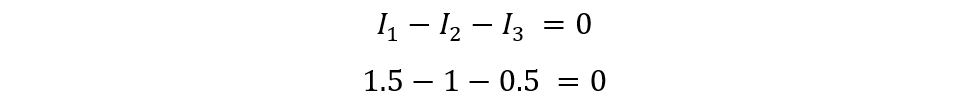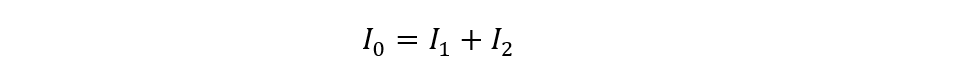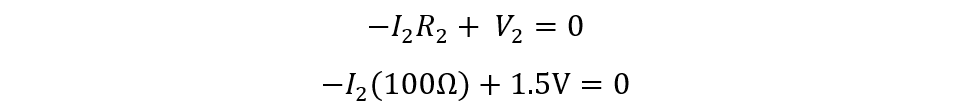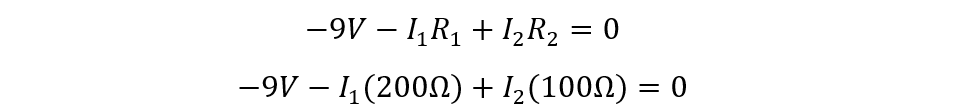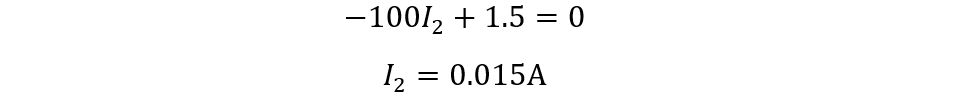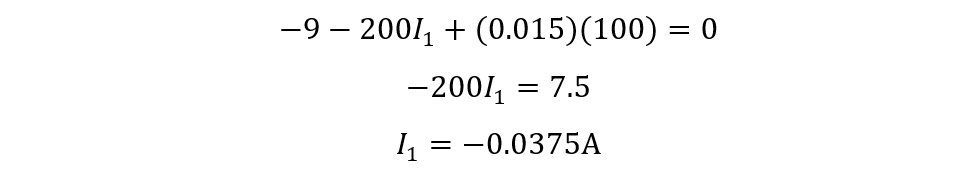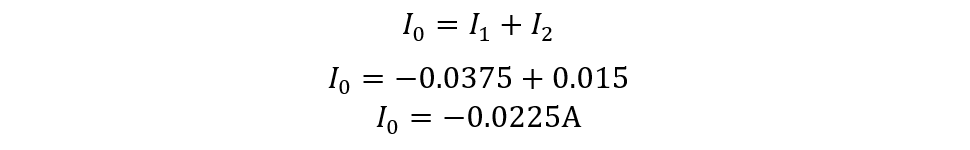Kirchhoff’s Current Law

Using Kirchhoff’s Current Law (KCL) we can understand how electric currents flow in a network of wires. It is established on the idea that charge is always conserved, meaning that it cannot be constructed or destroyed, only moved from one point to another. Kirchhoff’s current law has a background working like the law of conservation of energy.

This article will cover Kirchhoff’s Law, and we will study how this law can be applied in electrical circuits to solve complex voltage and current equations.

Quick Outline:

What Are Kirchhoff’s Laws?
What is Kirchhoff’s Current Law?
Example 1: Finding Current in Circuit
Example 2: Finding Current in Complex Circuit
Applications of Kirchhoff’s Current Law
Conclusion

What Are Kirchhoff’s Laws?

Kirchhoff’s laws were first represented in 1845 by German physicist Gustav Kirchhoff. Kirchhoff was a German physicist who made important assistance to the fields of optics, thermodynamics, electromagnetism, and spectroscopy. Kirchhoff’s laws are two basic laws of circuits in electricity that define the law of conservation of charge and energy.

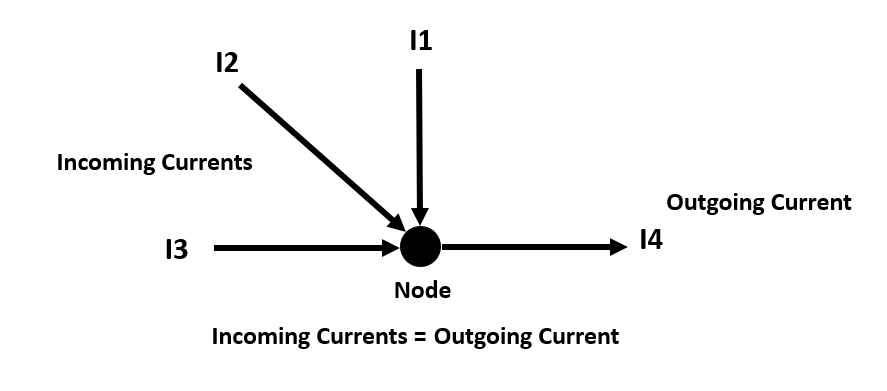
Kirchhoff’s Current Law (KCL): This rule states that the sum of all currents entering and leaving the junction is the same, it is also comprehended as the junction rule.

Kirchhoff’s Voltage Law (KVL): This rule states that all the voltages within any circuit closed loop are equivalent to zero. This law is also comprehended as Kirchhoff’s loop rule.

What is Kirchhoff’s Current Law?

KCL states that The total current flowing into a node must equal the total current exiting out of the node. A node is a point where two or more wires are connected, and a current is the rate at which charge passes through a wire. Algebraic sum means that we have to consider the direction of the currents as well as their magnitudes. For example, if two currents of 5 A and 3 A are there to enter a node, and one current of 8 A leaves the node, then the algebraic sum is 5 + 3 – 8 = 0 A, which is zero. This means that the circuit satisfies the KCL law, if it is not, you just need to balance the equation. The mathematical expression of KCL can be written as follows:

Where:

I_k is the current entering or leaving the node from branch k.
n is the number of connections to the node.
The sign of I_k is positive if the current is entering the node, and negative if the current is leaving the node.

Example 1: Finding Current in Circuit

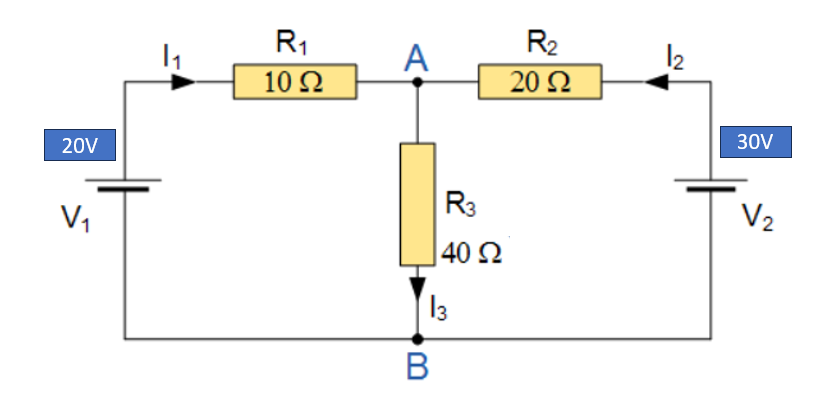
KCL can be used to find unknown currents in a circuit by applying it to each node and writing a system of equations. To illustrate how KCL works, let us consider a simple example of a circuit with three branches and two nodes, as shown in the figure below:

In this circuit, we have three currents: I₁, I₂, and I₃, and assume that the current is flowing in the path of the arrows drawn in the circuit. We can also label the nodes as A and B.

To apply KCL to this circuit, we need to write an equation that sums up all the currents entering and leaving node A. Since I₁ and I₂ are entering node A, we assign them positive signs. Since I₃ is leaving node A, we assign it a negative sign. The equation then becomes:

This equation tells us that the sum of I₁ and I₂ must be equal to I₃. For example, if we know that I₁=2A and I₂=3A, we can easily find that I₃=5A. Alternatively, if we know that I1=4A and I3=6A, we can easily find that I2=2A. And so on.

This is how we can use KCL to find the unknown currents in a simple circuit with one node. In the next section, we will see how to use KCL to analyze more complex circuits with multiple nodes and branches.

Example 2: Finding Current in Complex Circuit

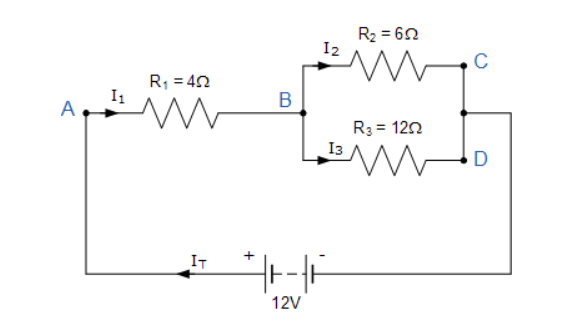
Now, let’s find the current in the following complex circuit:

The 12V supply voltage causes the total current I_T to flow around the circuit. At point A, the current I₁ is the same I_T, so the voltage drop across the resistor R₁ is I₁XR₁. The circuit has two branches, three nodes (B, C, and D), and two independent loops, so we can write the voltage drops around the loops as:

For loop AC, the equation for current will be:

Now for the Loop ABD

If we consider node B then according to Kirchhoff’s current law, the current:

This means that the current I₁ at node B splits into I₂ and I₃, so we can replace I₁ with (I₂ + I₃) in both loop equations and then simplify them so for loop ABC:

Now for placing the value of current I₁ in the equation for the loop ABD:

Now to find the value of currents, solve both equations by subtracting them after multiplying both equations with 4 we get:

Now placing the value of I₂ in the equation for the ABC, we can find the value of I₃:

Now find the value for the current I₁ will be 1.5 A so the equation according to the Kirchhoff current law will be:

Example 3: Finding Current in Circuit

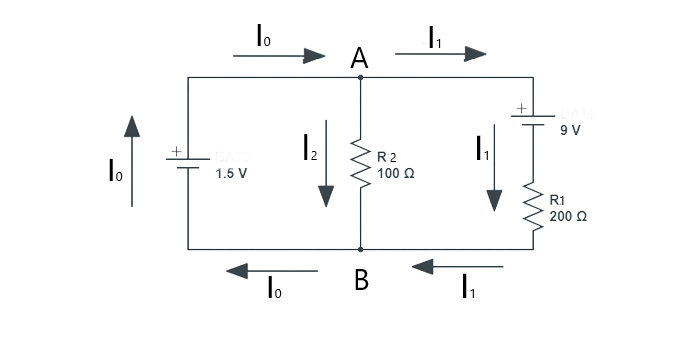
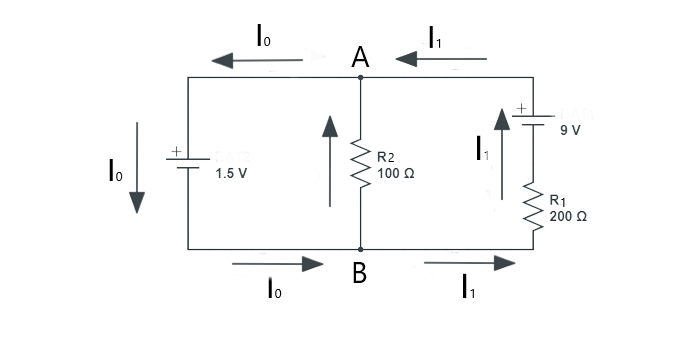
Consider a circuit having two resistors in parallel having resistances of 100 and 200 ohms respectively. The circuit has two voltage sources, one provides a voltage of 1.5 Volts and the other provides a voltage of 9 Volts. Find the current in the circuit.

Here A and B are the two junctions and the current direction of the circuit is arbitrary. So according to the junction rule, the sum of the current is the same both on the entering and leaving, so if we apply this rule to junction A:

Now if we apply the loop rule on the resistor R₁ and the voltage source V₂ then:

Now applying the loop rule to the second resistor R₂ and voltage source V₂ we get:

Now, from the first loop, we can calculate the value of I₂ from the first loop equation:

Now calculate I₁ using the value of I₂ in the second loop equation:

Since the direction of the current we chose was arbitrary here from the value of the current I₁ we can see the direction was wrong for the current I₁. So the current I₀ will be:

The circuit with the correct current direction will be:

Applications of Kirchhoff’s Current Law

Kirchhoff’s Current Law is a basic rule for analyzing the flow of current in a circuit. It can be applied to different types of electrical circuits, such as simple loop circuits, complex electrical circuits, and charging circuits. Some uses of Kirchhoff’s Current Law are:

Finding the current: Kirchhoff’s Current Law helps to find the current in various parts of an electrical circuit. It is also beneficial to know the direction of current flow in every circuit branch.
Solving DC circuits: Kirchhoff’s Current Law helps to solve the values of voltage, current, and internal resistance in direct current circuits.
Finding equivalent resistance: To calculate the current through each resistor in series and parallel combinations of resistors Kirchhoff’s law is used, which further helps in finding the equivalent circuit.
Studying junctions: Kirchhoff’s Current Law helps to study the flow of current at a junction or a node in a circuit. This helps in understanding the circuit behavior under different parameters.

Conclusion

To analyze and find the parameters of electrical circuits, there are different laws that are applied to circuits. Kirchhoff’s current law is one of them, which states that the sum of entering currents in a loop is equal to the sum of the currents leaving the circuit. This law is used in finding the current and voltage in the circuit and also helps in finding the equivalent circuits, which in turn makes it easy to understand and modify them.