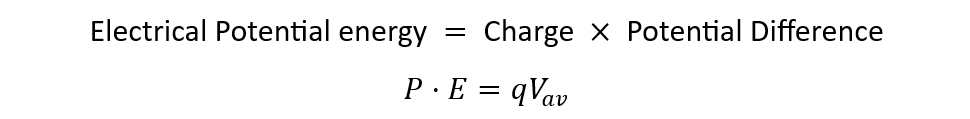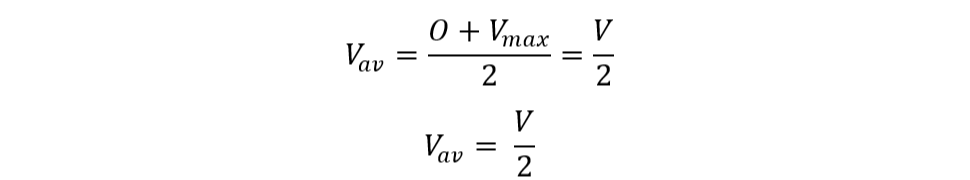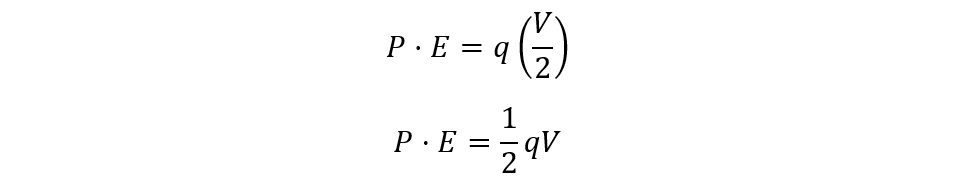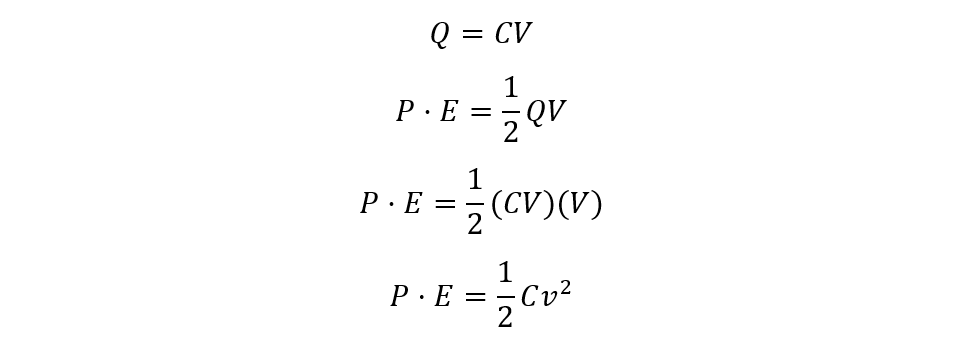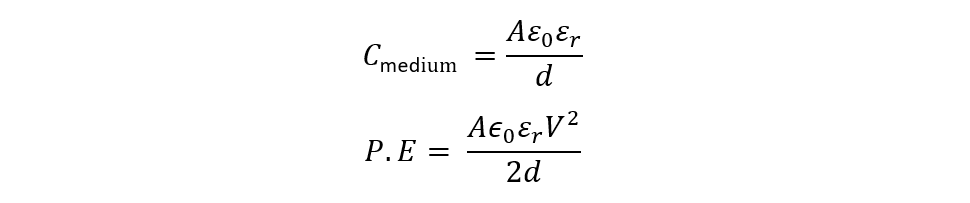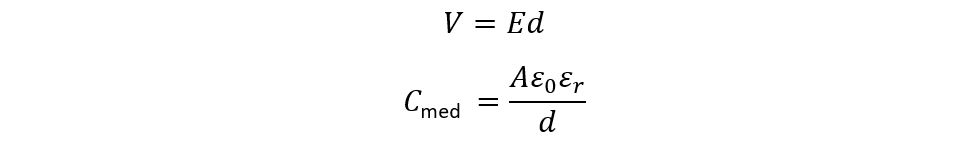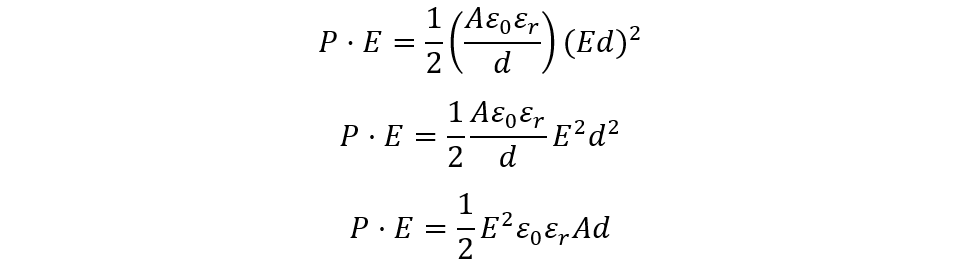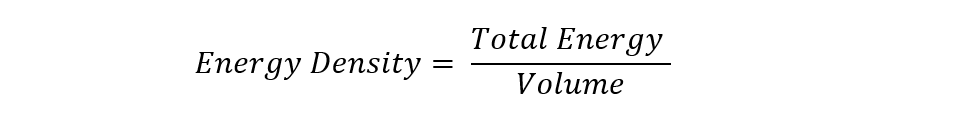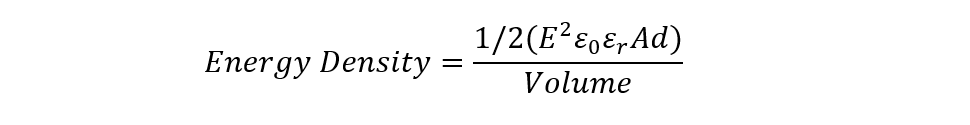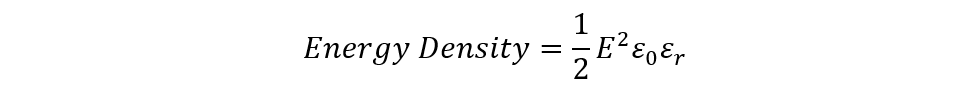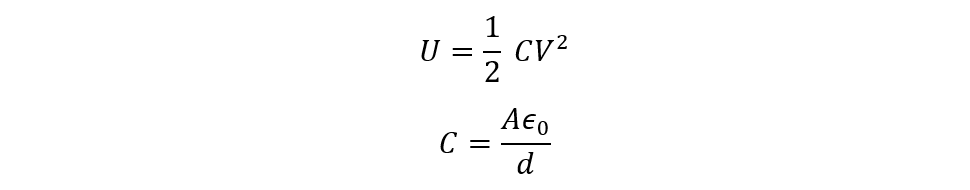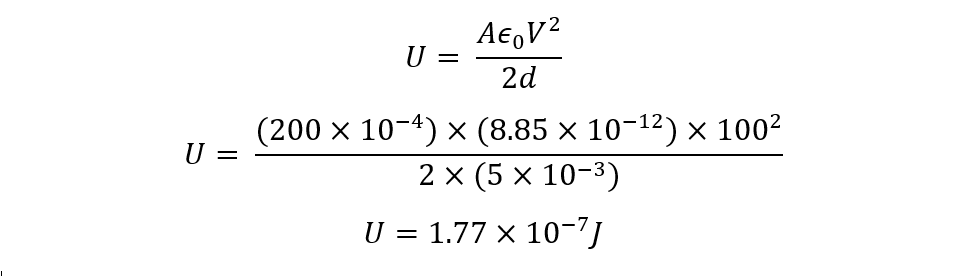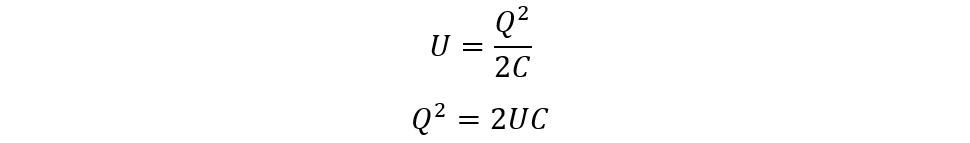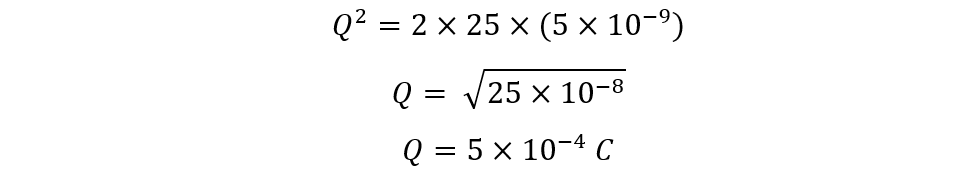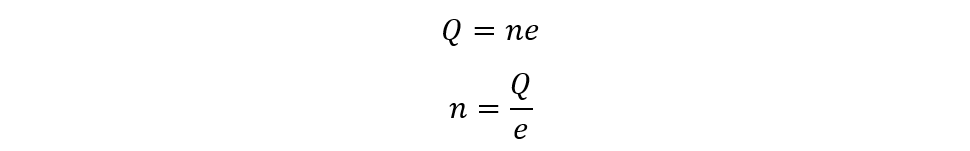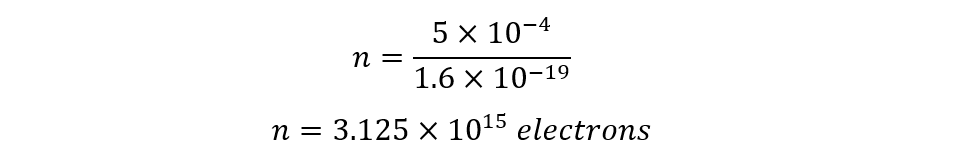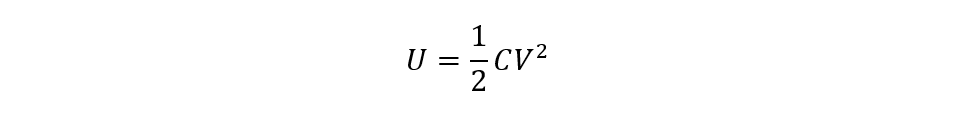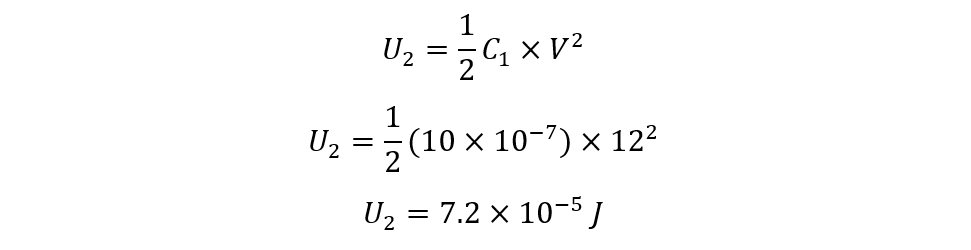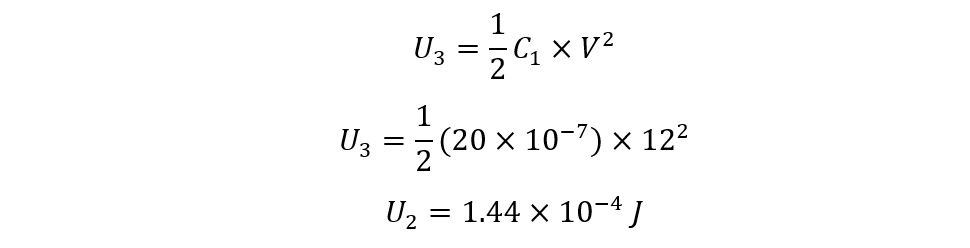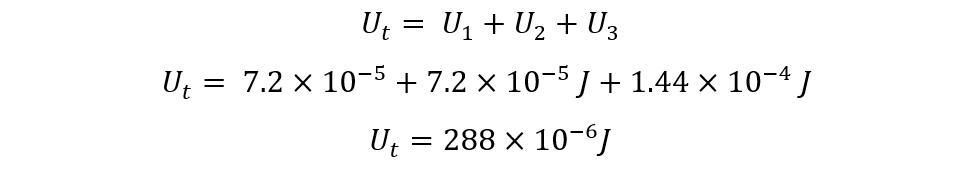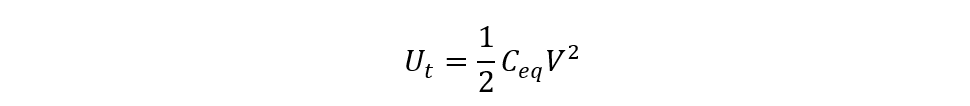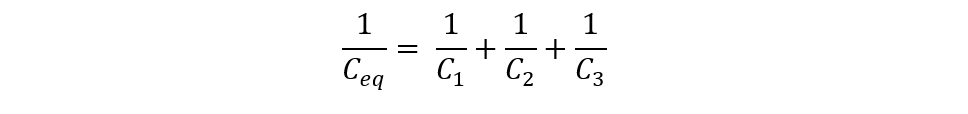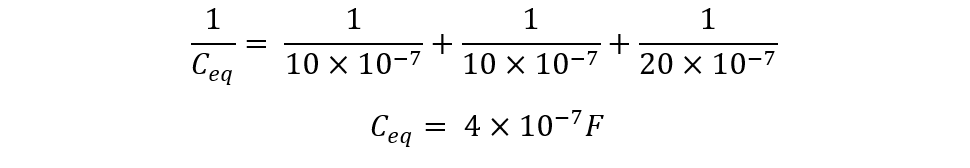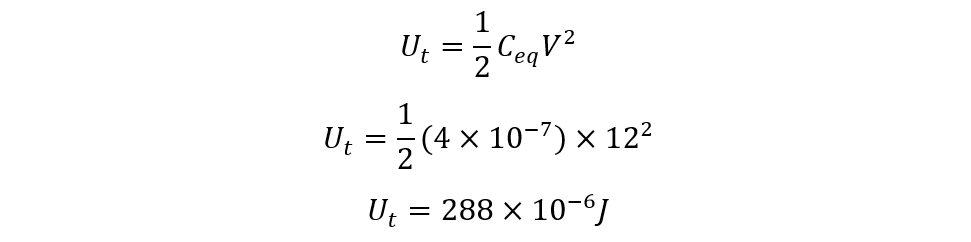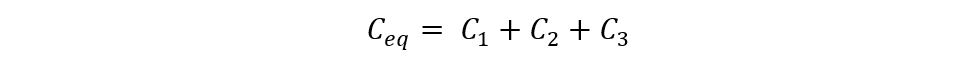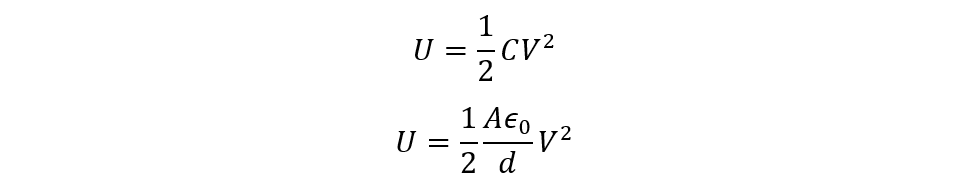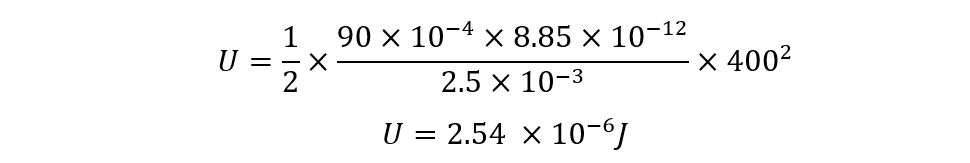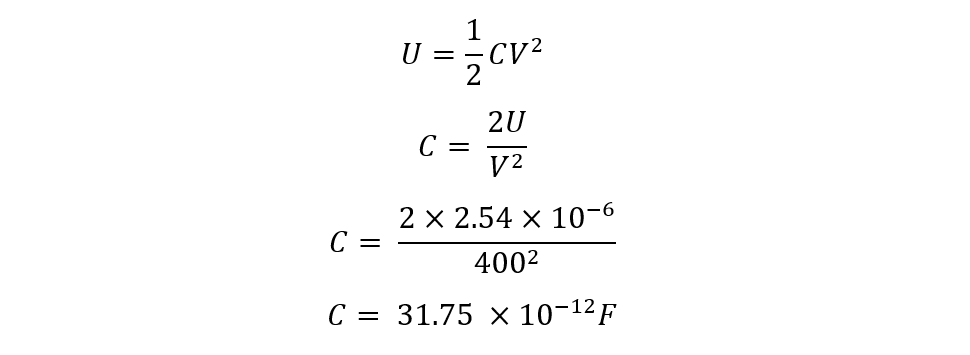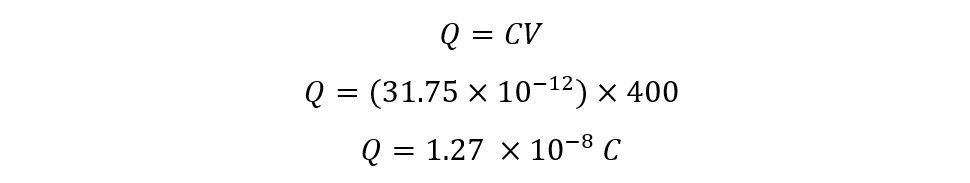How Does a Capacitor Store Energy

In electrical circuits and devices, there are two primary ways to store charge, one is through battery and the other is through capacitors. A battery can hold more charge for a longer time when compared with the capacitors. Moreover, the application of a capacitor is not only limited to storing a charge as it can be used for bypassing, filtering, rectification, providing boost, and more. Furthermore, the stored energy in both the batteries and capacitor creates an electric potential that drives the flow of electrons.

Outline:

Construction of a Capacitor
How Does a Capacitor Store Energy
Energy Stored in the Capacitor
Conclusion

Construction of a Capacitor

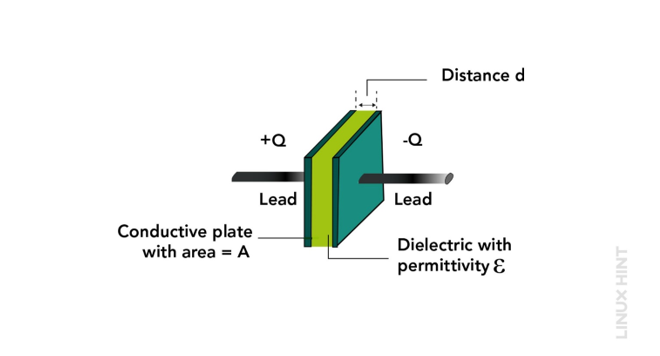
To understand how a capacitor stores energy, it is necessary to have a clear idea about its construction. Generally, the capacitors have the same construction but the material for the electrode and dielectric varies, and these parameters just alter the behavior of the capacitor. Every capacitor has an anode and cathode that act as its electrodes which are not electrically connected. In between these electrodes, there is an insulating medium that separates both of these electrodes often named dielectric:

The spacing between the plates of the capacitors depends on the required capacitance from the capacitor.

How Does a Capacitor Store Energy

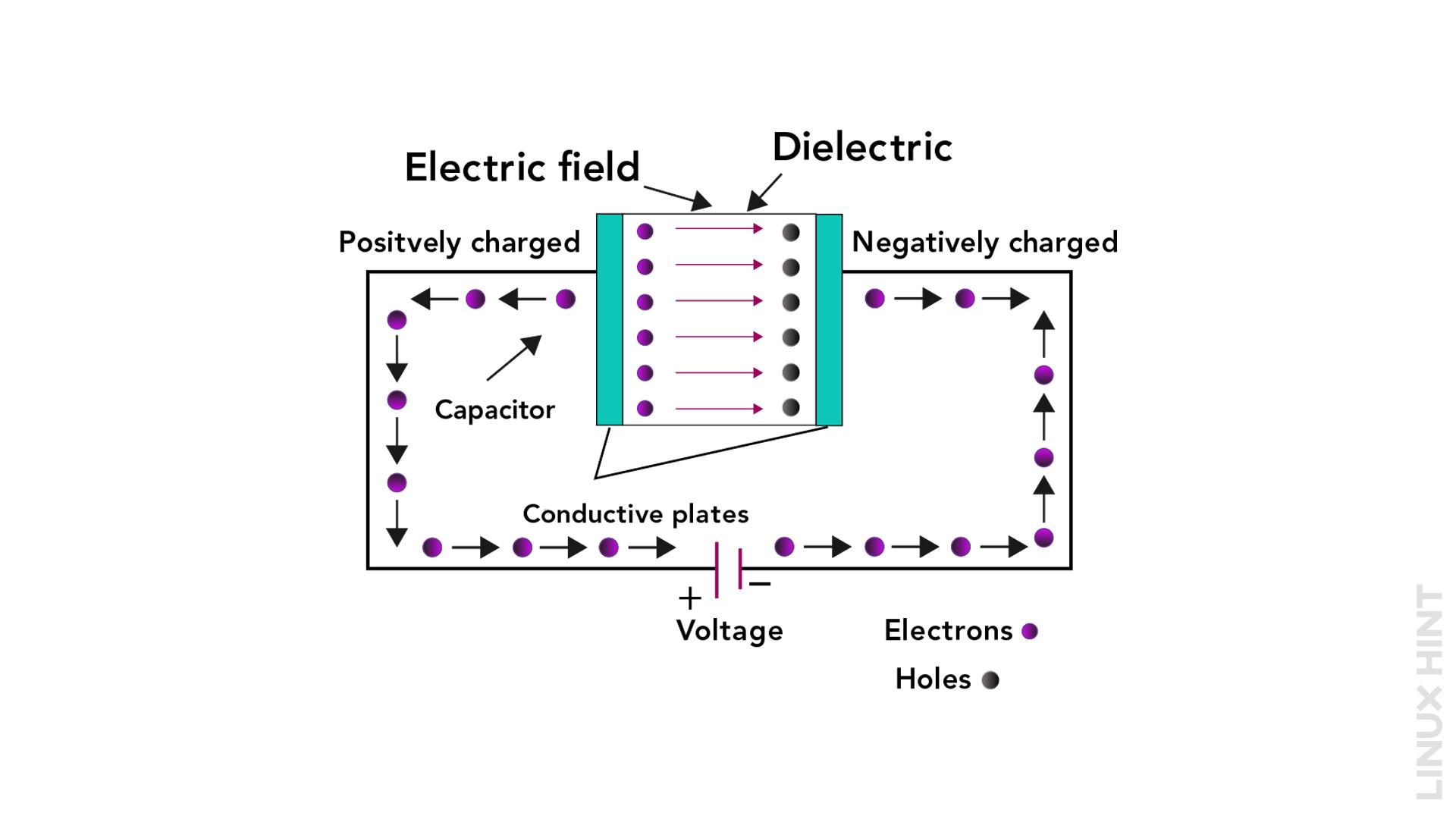
When a capacitor is connected to a supply the charge starts to flow from both electrodes of the capacitors and due to this an electric field is created between the two. This electric field is created due to opposite charges on the plates that try to equate the potential difference between the two points. Initially, a capacitor is at zero potential when it is fully discharged, so the charge from the supply keeps on flowing till the capacitor and the supply comes to the same potential. The energy utilized to move the charge carriers to the anode and cathode by the power supply is saved in the charges which can be used further while discharging the capacitor and this is how the capacitor stores its energy:

Now this energy stored in the charges can be released back to the circuit if any device is connected with it that is on low potential.

Energy Stored in the Capacitor

The energy stored in the capacitor is the sort of potential energy stored by the power supply in the charge carriers on both plates. So now we can write the equation for electrical potential energy stored in the capacitor like this:

Here the potential difference is constantly changing due to which we cannot take a fixed value, so here the average value of the potential difference is taken. Initially, the potential is zero when the supply is not connected and when the potential difference is increased upon connecting the supply. The potential difference keeps on increasing till it is at the same potential with respect to the supply, so we can calculate the average:

So now we can place the value of the average potential difference in the equation for potential energy:

Now we can write another formula for potential energy, as we know that the charge stored in the capacitor is a product of its capacitance and potential difference. So, by substituting the value of charge in the potential difference equation, we get:

Now as we know the equation for finding the capacitance, the capacitance of the capacitor is not known, but the other parameters are given then we can further write the equation for energy stored in the capacitor:

Both of the equations for the potential energy are based on the potential difference, but if the potential energy is taken in terms of an electric field, then the equation will be different. So, using the potential gradient and capacitance equation we can drive the equation:

Now place the values of capacitance and potential gradient in the previous equation:

Here E² is the electric field in the above equation, and all the equations we derived can be used to calculate the potential energy. However, the use of these formulas depends on the data provided. Energy density is another parameter that is associated with the energy stored in the capacitor, as the area of the plates is considered while measuring capacitance.

It is to be noted that energy density is not the total energy it is the energy that is stored in a per-unit volume so it can be written as:

Now place the equation for the total energy we derived previously:

The product of area and distance is volume, and this is because when we multiply the area by the third dimension, we get volume. So now we can cancel Ad from the volume and now the formula for the energy density will become:

Example 1: Calculate the Energy Stored in the Capacitor

Consider a parallel plate capacitor having a plate area of 200 cm² and the distance between the plates is approximately 5 mm. If a battery having a voltage of 100 Volts charges the capacitors, then find the total charge stored in a capacitor.

As we know the formula for finding the energy of a capacitor, and we need to know the capacitance, the formula for finding the energy stored can be:

Now if we place the value of capacitance in the energy stored equation and put the given values, then the energy stored in the capacitor will be:

Example 2: Find the Number of Electrons to Store a Charge in a Capacitor

Consider a parallel plate capacitor and store a charge of 25 J on one plate of the capacitor, how many electrons will be required if the capacitance of the capacitor is 5 nF?

To find the number of electrons on a plate of a capacitor first find the charge on the electrode, so for that use the equation of energy stored in a capacitor:

Now place the values of energy required and the value of the capacitance for the capacitor:

Now as we know energy stored in a capacitor is through the quantization of charge so we can write that charge is the product of a number of electrons and charge in one electron:

Now placing the values of the charge in a capacitor and charge on an electron, we will get the total number of electrons:

Example 3: Find the Energy Stored in Capacitors Connected in Series

Consider three capacitors that are connected in series and have an individual capacitance of 10 μf, 10 μf, and 20 μf respectively. If the power supply connected across the capacitor provides a voltage of 12 volts, then find the total energy of the capacitors and the energy stored in each of the capacitors:

Use the energy stored in the capacitor equation and find the energy stored in each capacitor:

For the First Capacitor:

For the Second Capacitor:

For the third Capacitor:

Now to find the total energy stored in the capacitors, sum up the individual values of the energy stored in each capacitor:

Another way to find the total energy is by finding the equivalent capacitance and then placing it in the equation to find the energy stored in the capacitor:

Since the capacitors are connected in series, the equation for finding the equivalent capacitance is:

Now, placing the values for individual capacitance:

Now find the total energy stored in the capacitors:

As you can see, the value of the total energy is the same using both methods.

Energy stored in capacitors in parallel Combination

If in case you need to find the total energy stored in capacitors that are connected to the parallel combination, then just calculate the equivalent capacitance in parallel using:

In series combination, the equivalent capacitance is lower than the individual capacitance of the capacitors, whereas in parallel the equivalent capacitance is higher than each of the individual capacitance.

Example 4: Find the Electrostatic Energy Stored in a Capacitor

Consider a parallel plate capacitor having an area of 90 cm² and the plates are separated by a distance of 2.5 mm. The power supply connected to the capacitor provides a voltage of 400 Volts, so how much electrostatic energy is stored in the capacitor? Also, find the charge on the capacitor.

Use the energy stored in the capacitor equation to calculate the electrostatic energy stored in the capacitor:

Now placing the values, we will get the value for the electrostatic energy:

Now we have the energy stored in the capacitor, so next find the charge in the capacitor first find the capacitance:

Now find the charge on the capacitor by multiplying the capacitance and voltage:

Conclusion

The charge stored on the plates of the capacitor is due to the potential difference between the plates of the capacitor. The capacitor stores the energy utilized by the power supply to move the ions to the plates of the capacitor. This energy can be named as the potential energy of the electrons because when there is a potential difference in a circuit these electrons will start to flow to compensate for the lower potential area using their potential energy provided by the power supply.