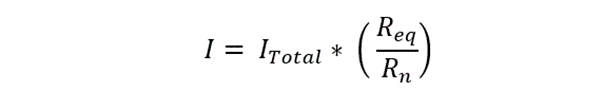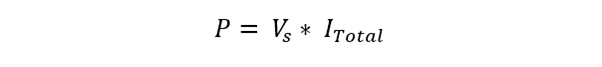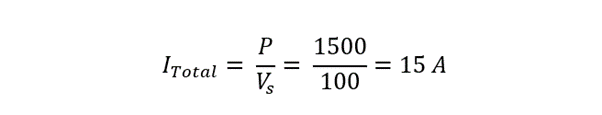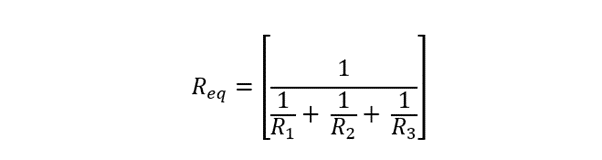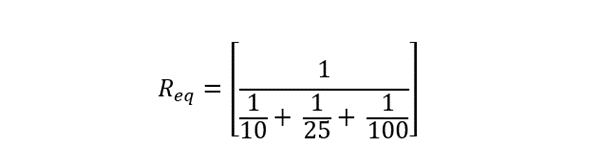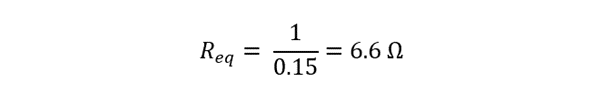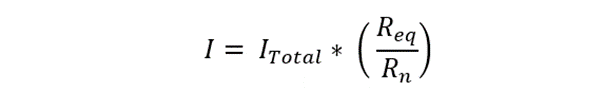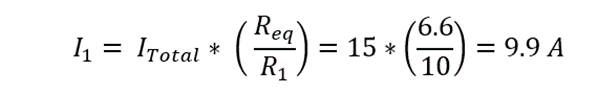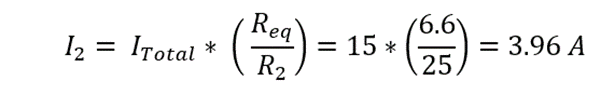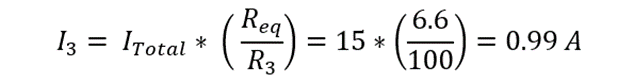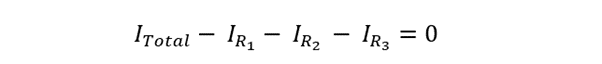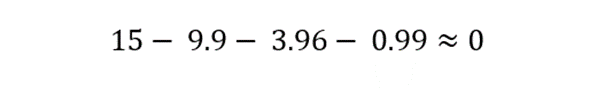A Guide to Current Divider Rule

In electrical circuits, the current divider rule is a fundamental principle that helps engineers and designers determine the distribution of current among parallel resistive elements. By utilizing this rule, it becomes easier to analyze complex circuits and calculate individual branch currents. In this article, we will explore the current divider rule, provide the equation for its calculation, and present an example to illustrate its application.

What is Current Divider Rule

The current divider rule is based on the concept that the total current flowing into a parallel circuit is divided among the branches in proportion to their respective resistances. It allows us to calculate the current flowing through a specific branch of a parallel circuit when the total current and resistance values are known.

The Equation for Current Divider Rule

The current divider rule can be mathematically expressed using the following equation:

Where I represent the current flowing through the branch (in Amperes), ITotal denotes the total current entering the parallel circuit (in Amperes). The R_eq represents the equivalent resistance, in Ohms, and R_n denotes the resistance of that respective branch.

Current Divider Rule Example

Consider an example to understand the application of the current divider rule:

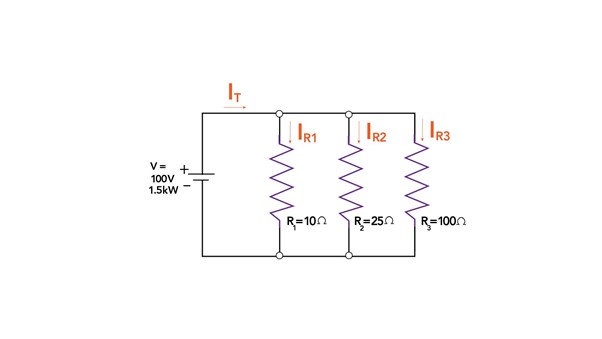
Suppose we have a parallel circuit with a voltage of 100 Volts and power of 1.5KW. The circuit consists of three branches, with resistances of 10 Ohms (R₁), 25 Ohms (R₂), and 100 Ohms (R3) respectively. We want to determine the current flowing through all the branches using the current divider rule.

Finding the total current of the circuit using:

Now finding the equivalent Resistance of the circuit using:

Now using the current divider rule for finding the branch current for all three branches:

Now to verify the branch currents calculations, we can use the Kirchhoff current rule:

Conclusion

The current divider rule is a useful tool in electrical circuit analysis, allowing engineers to determine the current distribution among parallel resistive elements. By utilizing the equation mentioned above, the current flowing through a specific branch can be calculated when the total current and resistance values are known.