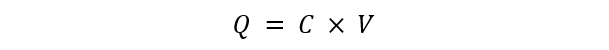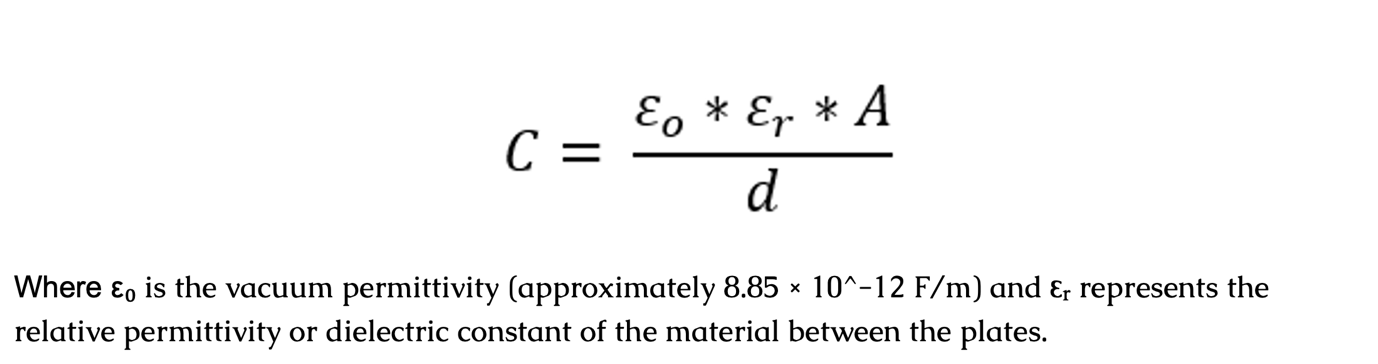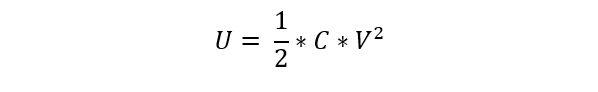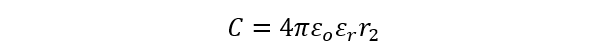Capacitors are fundamental components in the field of electronics and play a crucial role in various electronic circuits. Understanding the concepts of capacitance and charge is essential for anyone seeking to delve into the realm of electrical engineering. In this article, we will have a brief introduction to capacitors, explain capacitance, and delve into the equation that governs their behavior.
What is a Capacitor
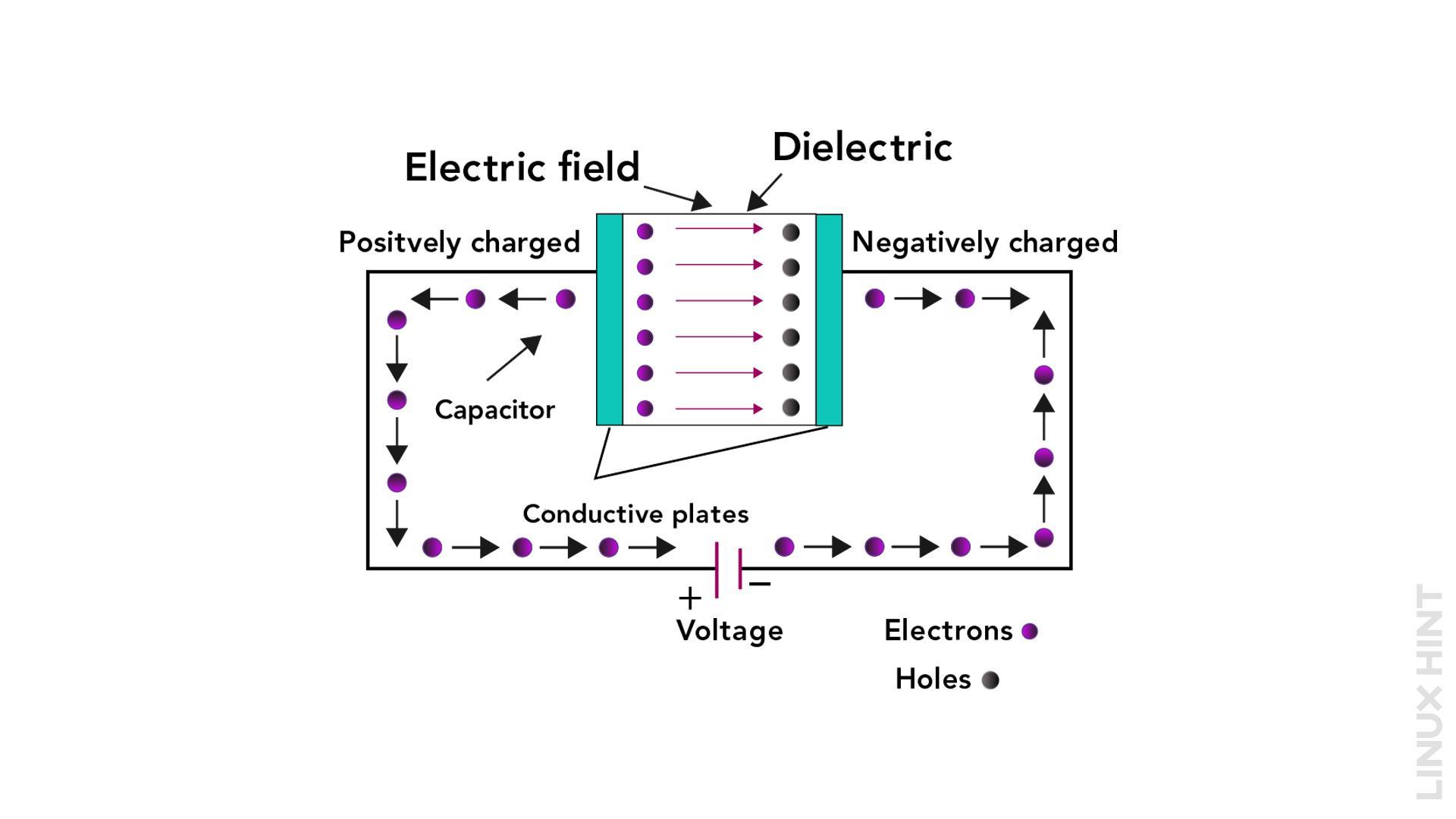
A capacitor is a passive two-terminal electronic component that stores electrical energy in an electric field. The structure of a capacitor comprises two conductive plates, usually composed of metal, which are positioned apart with a dielectric material in between them. When a voltage difference is applied across the terminals of a capacitor, it accumulates charge on its plates, creating an electric field between them.
What is Capacitance
Capacitance is a measure of how much electrical energy can be stored per unit of voltage across a device or component. The unit of capacitance is Farad.
What is Charge
The charge is described as the presence of electric energy. Its symbol is Q and its unit is Coulomb.
Working of Capacitors
When an electrical voltage is introduced across the terminals of a capacitor, the electric field established between the plates initiates the motion of electrons. The capacitor’s negative plate becomes a collection point for electrons that have moved from the voltage source’s negative terminal.
Simultaneously, an equal number of electrons leave the capacitor’s positive plate and return to the positive terminal of the voltage source.
This accumulation and redistribution of charge continue until the capacitor is fully charged, at which point the flow of electrons ceases, charge stored in a capacitor can be determined using the equation:
In the given equation, “Q” symbolizes the charge accumulated within the capacitor, “C” denotes the capacitance, and “V” represents the applied voltage across the capacitor.
This equation displays a proportional relationship between the capacitance and applied voltage, showing that the amount of charge held in a capacitor is directly related to both of these variables. Hence, increasing either the capacitance or the voltage will result in a higher charge accumulation.
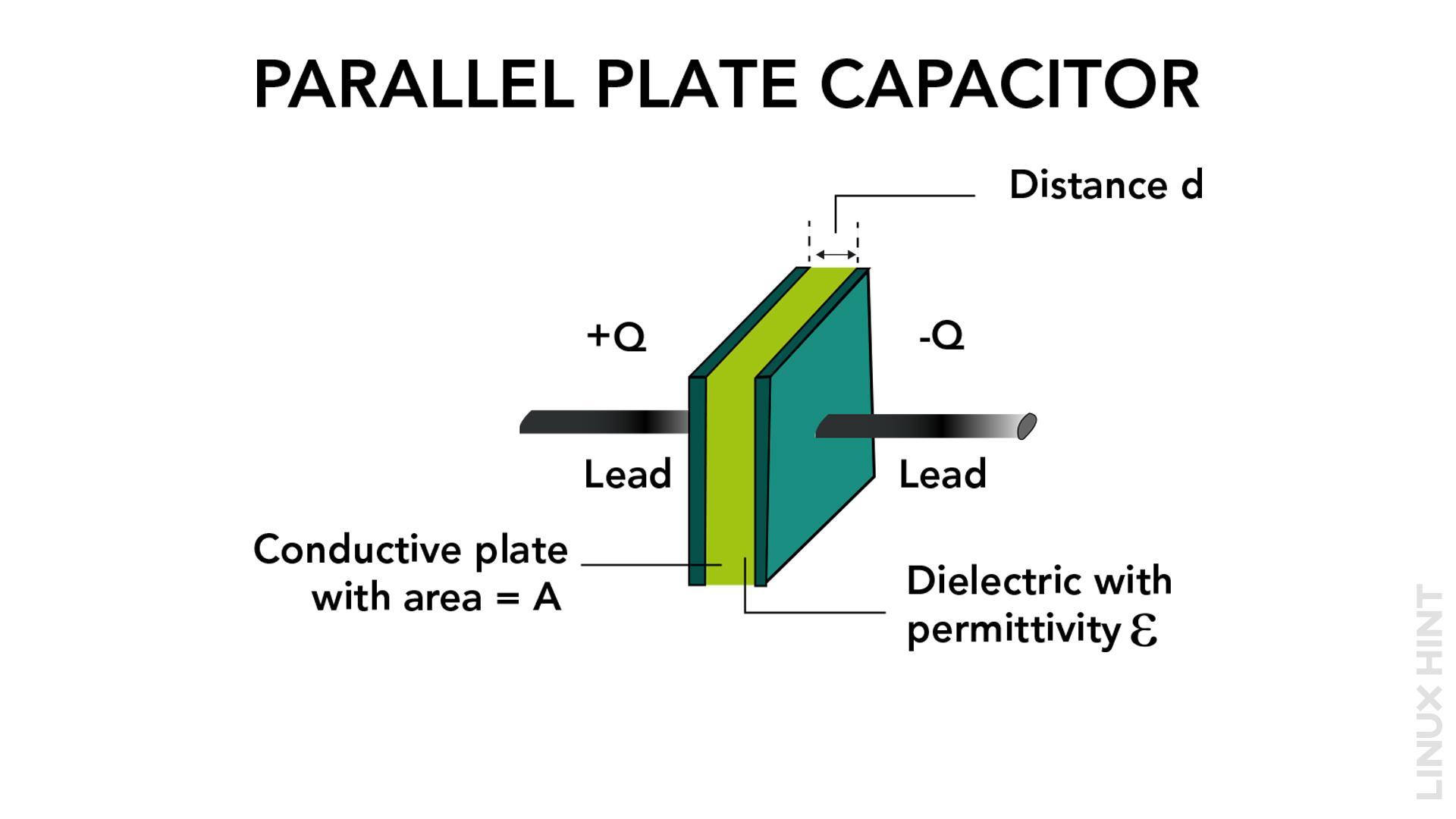
Capacitance of a Parallel Plate Capacitor
The capacitance of a capacitor is determined by the surface area of the plates (A) and the separation distance (d) between them, with both factors impacting its overall capacitance. The larger the plate area, the greater the capacitance, while a smaller distance between the plates leads to increased capacitance. This relationship is described by the equation:
Capacitors possess the capability to store electrical energy, whereby the quantity of energy stored (U) is directly proportional to both the square of the applied voltage (V) and the capacitance (C) of the capacitor. The equation for energy stored in a capacitor is given by:
Knowing the energy stored in a capacitor is vital for designing circuits, especially in applications where energy release or instantaneous power requirements are important.
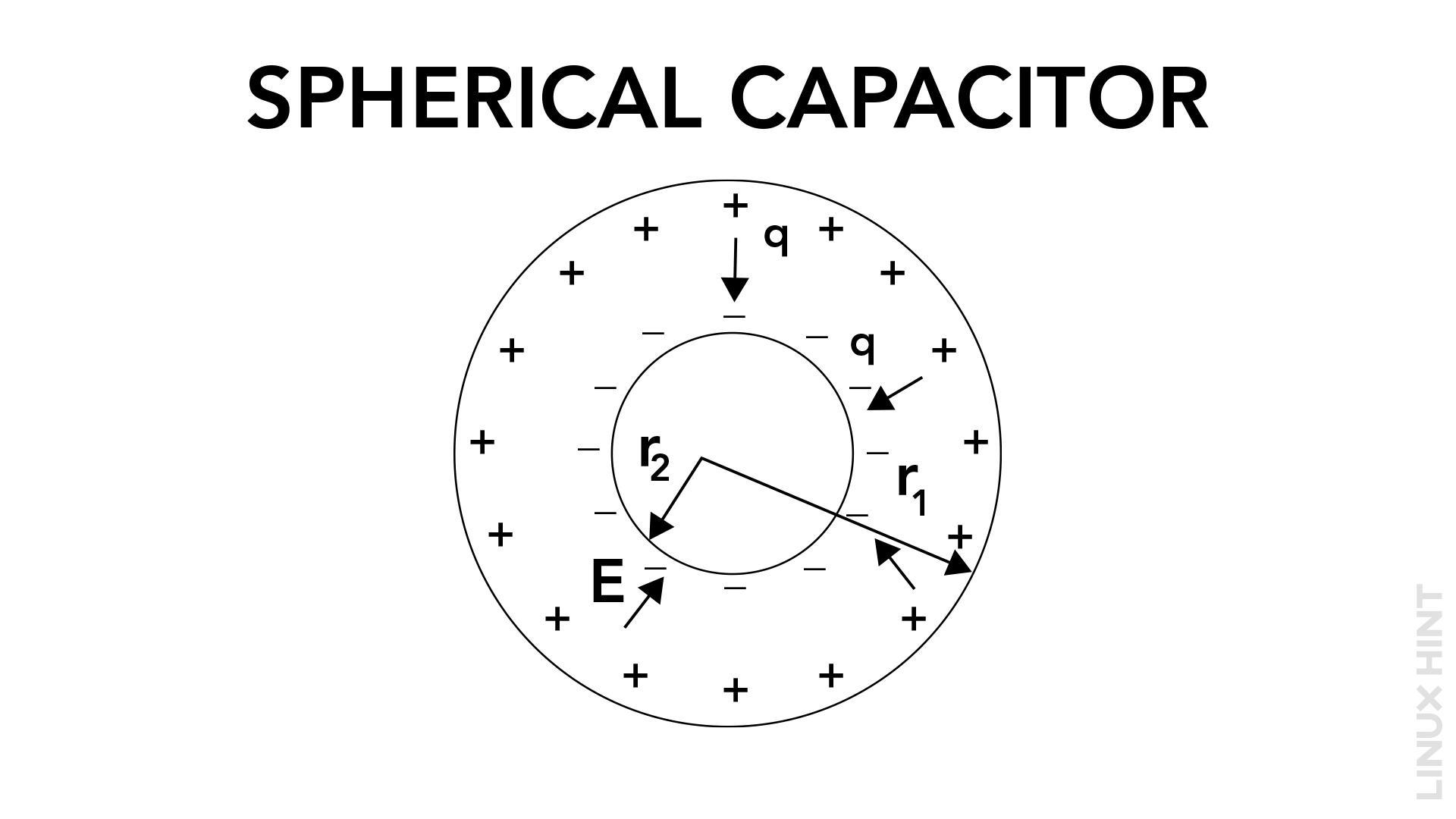
Capacitance of a Spherical Capacitor
To calculate the capacitance of a spherical capacitor, you need to know the radius of both the inner and outer conductive spheres. The shape of the capacitor and the permittivity of the material positioned between the spheres control the capacitance. The formula for calculating the capacitance of a spherical capacitor is:
On the other hand, the symbol “εᵣ” is utilized to represent the relative permittivity or dielectric constant of the material located between the spheres. Additionally, “r₁” denotes the radius of the inner sphere, while “r₂” signifies the radius of the outer sphere.
By substituting the values of the radius and the permittivity of the material, you can calculate the capacitance of the spherical capacitor. It’s worth noting that if the inner sphere has a negligible radius or is considered a point charge, the capacitance formula simplifies to:
In this case, the capacitance is solely determined by the radius of the outer sphere and the permittivity of the material.
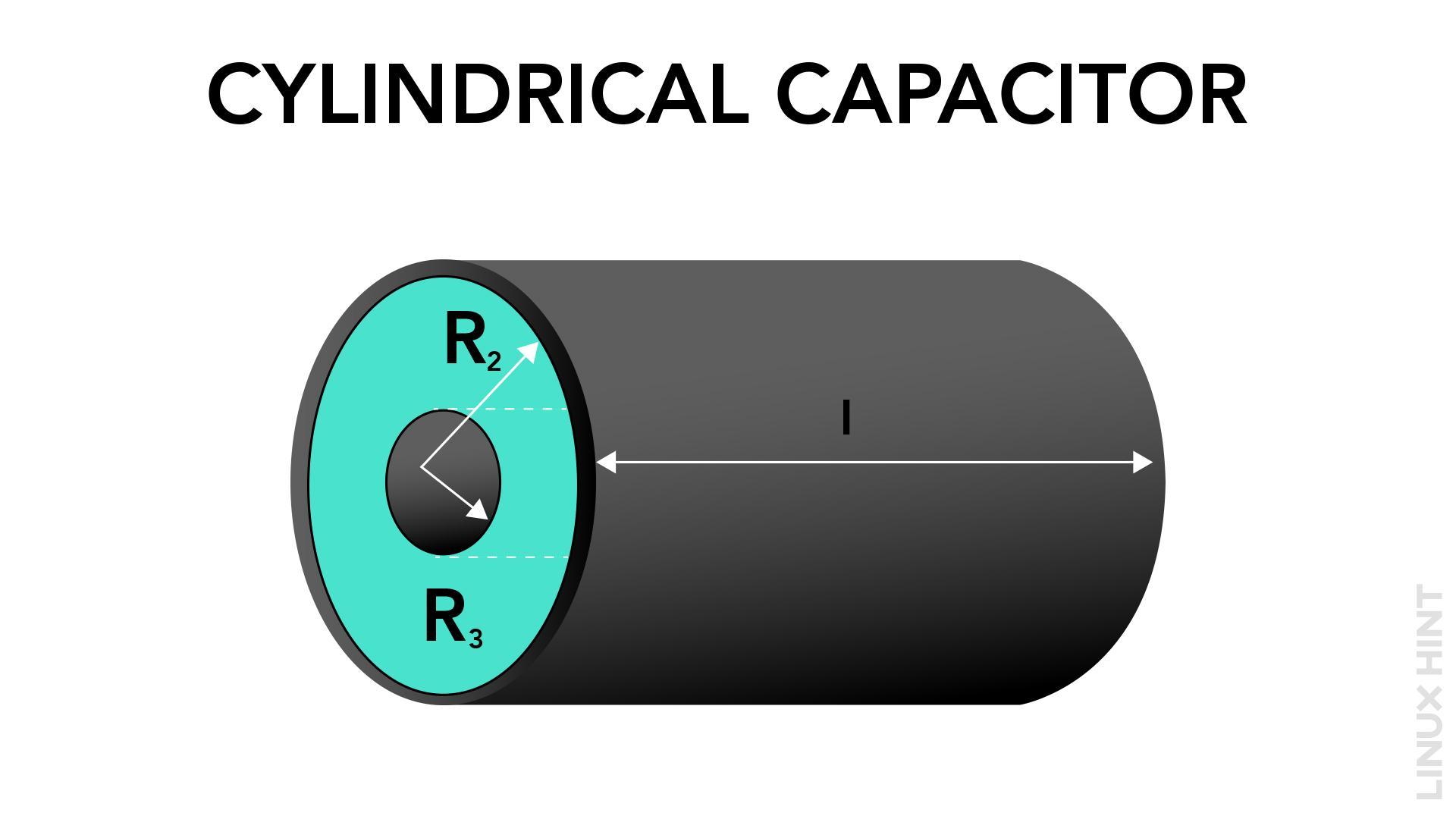
Capacitance of a Cylindrical Capacitor
To calculate the capacitance of a cylindrical capacitor, you need to know the length of the capacitor (L), the radius of the inner conductor (r₁), and the radius of the outer conductor (r₂). The shape of the capacitor and the permittivity of the material positioned between the spheres control the capacitance. The formula for calculating the capacitance of a cylindrical capacitor is:
On the other hand, the symbol “εᵣ” is utilized to represent the relative permittivity or dielectric constant of the material located between the spheres. Additionally, “r₁” denotes the radius of the inner sphere, while “r₂” signifies the radius of the outer sphere.
Conclusion
Capacitors are crucial components when it comes to electronics, enabling energy storage and voltage regulation. Capacitance, measured in farads (F), quantifies a capacitor’s ability to store charge. It is directly proportional to the charge stored (Q) and inversely proportional to the voltage (V) across the terminals of the capacitor.