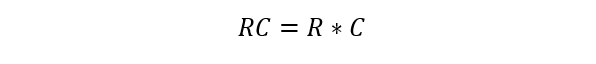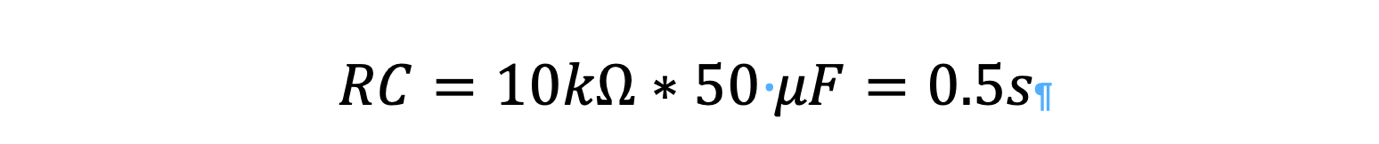In electronic circuits, the resistor-capacitor (RC) time constant is a crucial parameter that determines the behavior and timing characteristics of RC circuits. The calculation of the RC time constant is crucial in comprehending circuit behavior and designing systems with precise timing needs. It quantifies the rate at which a capacitor charges or discharges in the presence of a resistor, enabling accurate analysis of circuit response. In this article, we will delve into the concept of the RC time constant, explain its significance, and provide a step-by-step guide on how to calculate it.
RC Time Constant
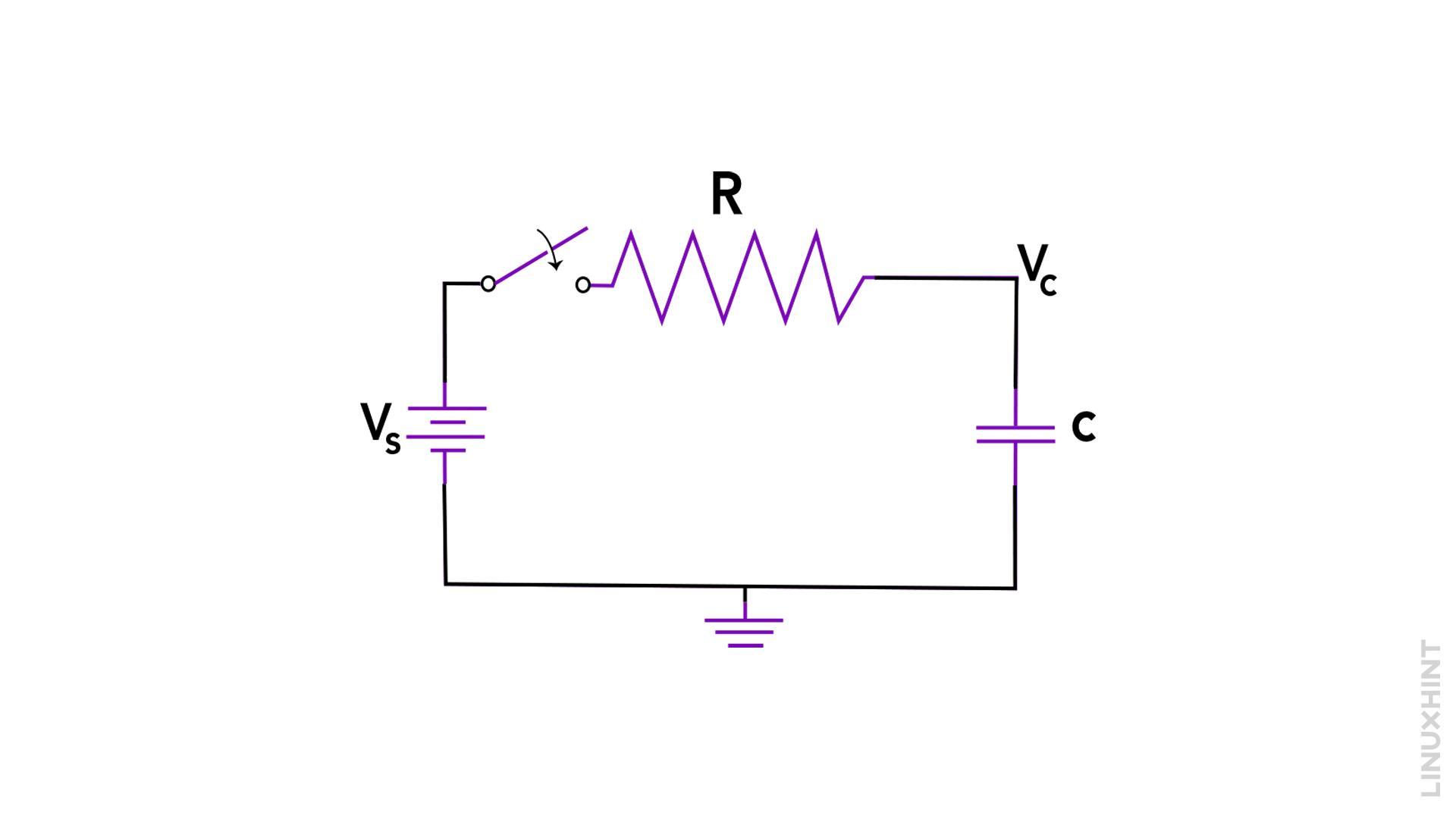
In an RC circuit, the RC time constant (represented by the symbol t) signifies the duration required for a capacitor to charge up to around 63.2% (1 – 1/e) of its maximum charge or discharge down to approximately 36.8% (1/e) of its initial charge. The circuit’s resistance (R) and capacitance (C) are multiplied to come up with this time constant.
How To Calculate Resistor Capacitor Time Constant
To determine the RC time constant, you can utilize the following step-by-step procedure:
Step 1: Identify the values of the resistance (R) and capacitance (C) in the circuit and ensure they are expressed in the appropriate units (e.g., ohm for resistance and farad for capacitance).
Step 2: Multiply the resistance (R) and capacitance (C) values together:
Step 3: This multiplication’s result represents the circuit’s RC time constant (t).
Example Calculation
Consider an example where a circuit has a resistor (R) of 10 kilohms (10kΩ) and a capacitor (C) of 50 microfarads (50μF), so the resistor-capacitor time constant will be:
Therefore, this circuit’s RC time constant (t) is 0.5 seconds.
Conclusion
The RC time constant is a fundamental parameter in electronic circuits, determining capacitors’ charging and discharging behavior through resistors. By understanding and calculating the RC time constant, engineers can accurately predict circuit response times, design timing circuits, optimize filtering characteristics, and estimate energy storage and power dissipation.