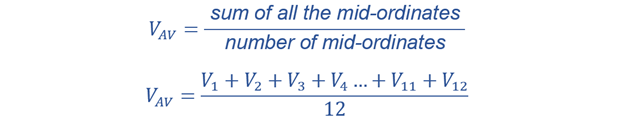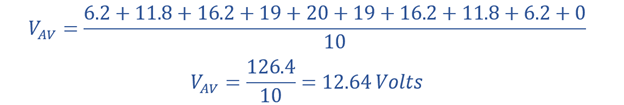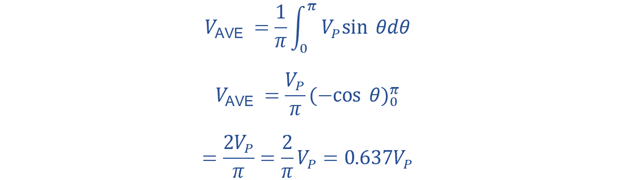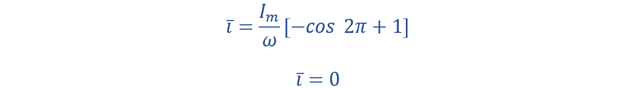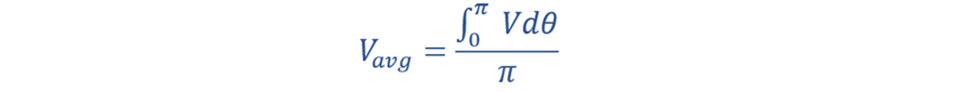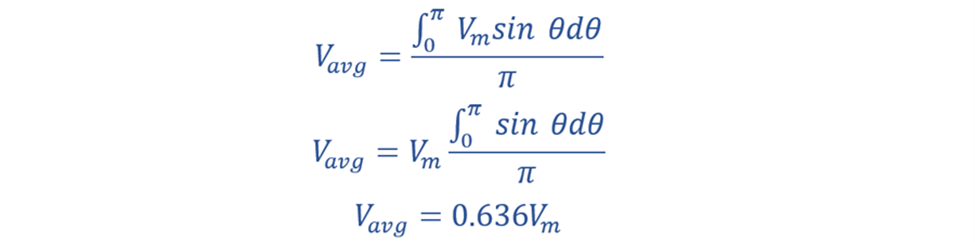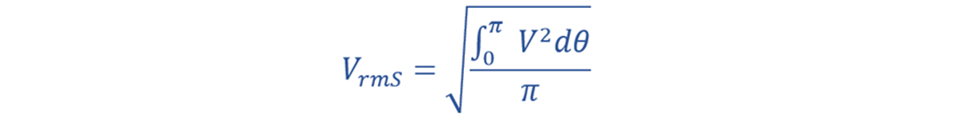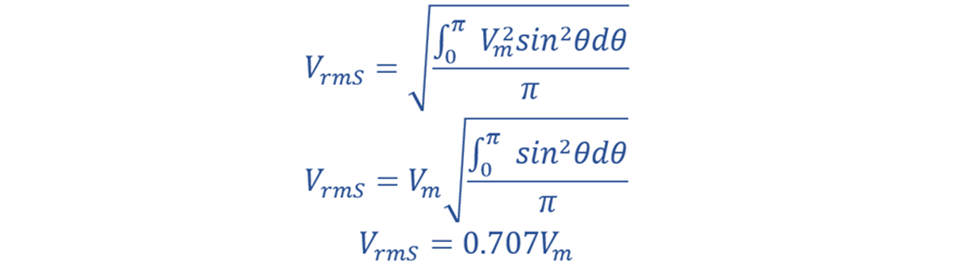The average value of an AC waveform is 0.637 times the peak value. The sine wave average values for both the current and voltage are equivalent to 0.637 multiple with the peak value. The average value of any AC waveform is zero. This is because the AC signal is continuously shifting and changing its half. An AC sinusoidal signal alternates from the positive cycle to the negative cycle values.
To find the alternating or AC waveform average voltage, you have to integrate the current and voltage values over the half cycle. After that, you have to divide their result by half-cycle base length. Therefore, the average value of an AC waveform is considered an important concept in electronics. Using the average value, you can find the behavior of alternating currents and voltage signals.
In this article, we will find out how the average value can be calculated in different instances of an AC signal. Further, we will also do the comparison of average values of different AC signals at various times. To give you a clear understanding of the AC waveform topic, numerical problems are also included to give you a better understanding of the topic.
Quick Outline
What is the Average Value of a Sinusoidal AC Wave
Both the average voltage from the AC signal and its equivalent DC signal voltage have the same amount of power. The average voltage of a sinusoidal AC wave is calculated by finding the area under the curve of one-half cycle and dividing it by the time period of that half cycle.
The method for finding both the average voltage and RMS value of the AC signal is almost similar but with some differences. Here, in the AC waveform average voltage calculation, we do not take the square of the AC signal instantaneous values. The square root of the mean sum values is also not calculated.
In a periodic waveform, the region above the horizontal axis is positive, and below it is negative. Therefore, we can say that the average value for a symmetrical AC signal across the full AC signal or entire 360° time period is zero (0). This zero average arises from the balancing act between the equal areas above (positive half cycle) and below (negative half cycle) the axis. This will result in canceling each other out. In simpler terms, the mathematical comparison of these two areas results in the negative area nullifying the positive area, which results in a net-zero average value.
To determine the average value of an AC signal, like a sine wave, you have to focus on just one-half of a cycle. This choice recognizes that the average value over an entire cycle remains zero, irrespective of the peak amplitude.
The terms that we are studying here, like the Average Voltage, Mean Voltage, as well as average current, can be used in both AC signals and for the DC rectification calculations. The average value of the AC signal can be represented as VAV for the voltage and IAV for the average current value.
Finding Average Voltage Using AC Waveform Graph
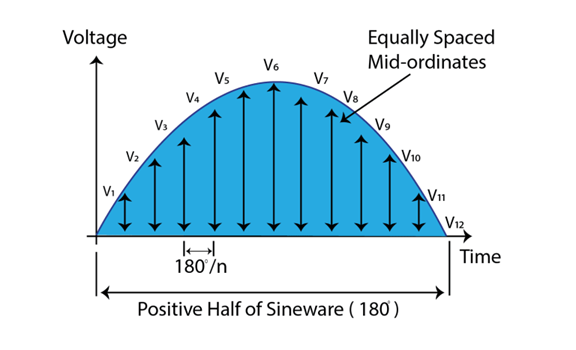
To find the average or mean voltage of a waveform, we can use the graphical method. Let’s focus on the positive half cycle. We can divide the positive half of the waveform into n equal parts or mid-ordinates. The width of each mid-ordinate is N° degrees (or t seconds). Its height is equal to the instantaneous value of the waveform at that point on the x-axis.
We can take samples of the waveform’s value at equal intervals to estimate the average or mean voltage graphically.
The average voltage (VAV) is equal to the mean value of the voltage signal over one cycle. To calculate it, we divide the sum of the mid-ordinate values of the voltage waveform by the number of mid-ordinates used. The mid-ordinate values are the voltages at the middle of each segment of the waveform. We add them up from V1 to V12 and then divide by 12 which is the number of mid-ordinate values, this will give us the average voltage of the sinusoidal waveform.
Let’s say that an alternating voltage that changes size every moment has a maximum size or peak value of 20 volts over the one-half cycle:
So the average value can be given as:
The average voltage for one half-cycle of the sinusoidal waveform is equal to 12.64 volts.
Finding Average Voltage Using Analytical Method
For a periodic waveform with identical halves, whether sinusoidal or non-sinusoidal, the average voltage over a complete cycle is zero. You can find the average value of a sinusoidal waveform by adding up the voltage values over half a cycle. But for a complex or non-symmetrical wave, you need to use math to calculate the average voltage (or current) over the whole cycle.
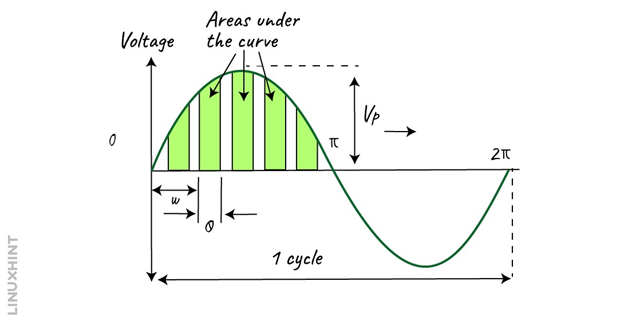
Mathematically, you can calculate the average value by approximating the area under the curve at various intervals relative to the distance or length of the base. This approximation of the sinusoidal waveform can be achieved by using the small triangles or rectangles inside the half cycle of a sinusoidal waveform.
By approximating the areas of rectangles beneath the curve, we can get a preliminary estimate of each area. Summing up these areas will help us to determine the average value. A more accurate result can be achieved with an increasing number of smaller rectangles as these rectangles approach the 2/π.
You can use several approximation methods to find the area under the curve or average voltage. These approximation methods include the trapezoidal rule, mid-ordinate rule, or Simpson’s rule. All of these can give you the area under the curve. The mathematical expression of the area under the positive half cycle of a periodic wave can be given by V(t) = Vp.cos(ωt) with a period of T. To calculate its value, we have to take the integration of the expression from period 0 to π, which is equal to one-half cycle of a sinusoidal waveform.
Consider the limits of integration from 0 to π, as we are determining the average voltage over one-half of a cycle. The area under the curve is 2VP. This is the area for either the positive or negative half-cycle of a sinusoidal waveform. You can use this to find the average value of the positive (or negative) part. To do this, divide the area by half the period. This is the same as integrating the sinusoidal quantity over half a cycle.
For example, if the instantaneous voltage of the alternating signal is V = Vp.sinθ and the period is given as 2π, then:
Average Voltage and Current Equation
The average voltage of an AC waveform is the value obtained by dividing the area under the curve by the length of the cycle.
For a sinusoidal waveform, the average voltage is equal to 0.637 times the peak voltage. This means that the average voltage of a sine wave with a peak voltage of 340 Volts is:
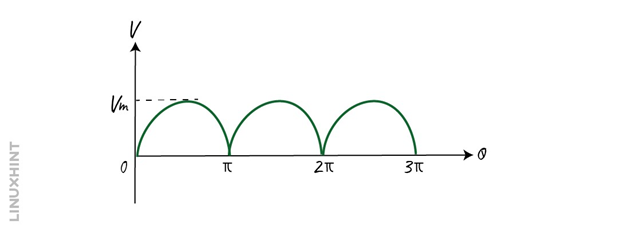
The RMS voltage, which is the effective voltage of an AC waveform, is equal to 0.707 times the peak voltage. The average and RMS voltages of a sine wave are shown in the figure below:
Note: The factor of 0.637 is only valid for a sinusoidal waveform. Other waveforms, such as Sawtooth or triangle, have different factors.
The average voltage (VAV) in a sinusoidal waveform can be determined by multiplying the peak voltage with the constant 0.637. This constant value is equivalent to two divided by pi (π). This average voltage of a sinusoidal waveform is also known as the mean value. It relies on the waveform’s magnitude and remains unaffected by frequency or phase angle.
You can show the average value of a sinusoidal waveform as a DC value by looking at the area under the curve and the time. This makes it easier to represent the waveform as a constant, direct current (DC) value.
Overall, the average value is zero for a complete cycle. The positive average area cancels out the negative average area (VAVG – (-VAVG)). So, you will get the zero answer for the average voltage when obtained over one complete cycle of a sinusoidal signal.
As demonstrated in the graphical example, we have noticed that the peak voltage (Vpk) was given as 20 Volts. Similarly, the analytical method calculates the average voltage as follows:
This value aligns with the graphical method.
You can find the peak value from the average voltage by dividing it by a constant. For example, if the average voltage is 65 volts, the peak value (Vpk) of the sinusoid is:
Note that the multiplication of peak or maximum value by the constant value 0.637 should only be done in the case of sinusoidal waveforms.
Average Value Comparison of Different Waves
The average value of AC is obtained when we convert the AC to DC by using a rectifier. The output of the rectifier which is a converted AC is called the average value of AC. You can use two methods to find the average value of a sinusoid: the graphical method or the standard sinusoidal equation.
The standard sinusoidal equation gives the average value of AC as:
Where Im represents the peak value of the sinusoidal wave.
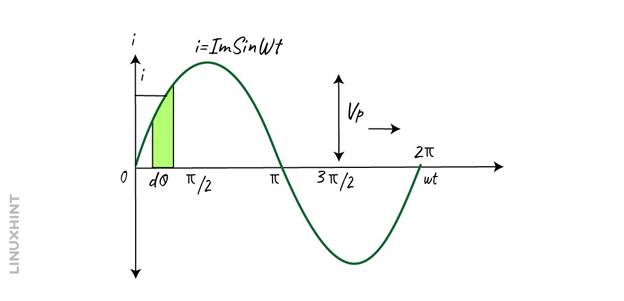
Now we will calculate the average value of the AC sinusoidal signal. For that, consider the first half of the following sinusoidal wave.
The average value of an AC signal is found by dividing the area under the graph of the sine wave by the total time period for which the area has been found.
Average Value of Full AC Cycle
The average value for the full sinusoidal AC cycle is given as:
The time period is linked with the angular frequency as:
Substitute the value of Time T in the above equation:
So, from the above equation, it is calculated that the average value of the full cycle of the AC waveform will be zero.
Average Value of Half AC Cycle
To calculate the average value of half an AC cycle of a sinusoidal waveform, you need to integrate the function over the given interval:
The formula for the average value of AC is:
For a complete sine wave, we determined that the average value is zero. This is due to equal amounts of current in the positive and negative cycles. This flow of current is in opposite directions and will cancel each other and result in a zero average value for a full sinusoidal wave. The same principle will apply to the alternating voltage, leading to the formula:
This above formula is true for a half cycle. For the entire cycle of the AC wave, the average value of voltage remains zero.
Average Value of DC Signal
A DC waveform, like a constant DC signal, has the same average value as its constant, RMS, and peak values. You can find the average value of a DC waveform by using this formula:
Where Vavg is the average value and Vdc is the constant value of the DC signal. This is important for things like power supplies and battery systems, where you need a steady voltage level. The average value of a DC waveform is a basic parameter in many engineering applications, and it helps you understand how different waveforms work.
Sinusoidal Average Value Calculation
Find the Average value and RMS value of the following waveform.
1. Average Value Vavg:
The formula for average value is given by:
Applying it to your waveform (VmSinθ), after integration, you get (Vavg=0.636 Vm).
2. RMS Value VRMS:
The formula for the root-mean-square (RMS) value is:
Applying it to your waveform (VmSinθ), after integration, you get (VRMS=0.707 Vm).
The average value is approximately 0.636 times the maximum value Vm, and the RMS value is approximately 0.707 times the maximum value Vm for the given waveform.
Conclusion
The average value of an AC waveform is an important parameter in electrical engineering. You can easily determine the behavior of alternating current and voltages using the average value of an AC sinusoidal signal. The peak value of a sinusoid is 1.57 times the average value. However, the average value of any AC signal is zero. This is because the AC signal keeps changing from positive to negative peak values.
You can find the average value of an AC waveform by averaging the voltage or current values over one cycle. For a sinusoid, you can do this by integrating the voltage or current values over half a cycle. Then, divide by the length of the half cycle. You can make the average value more accurate by using many small rectangles. The average value is used in rectifier-type multimeter circuits. Average values indicate the RMS values of voltage or current for sinusoidal waves only.