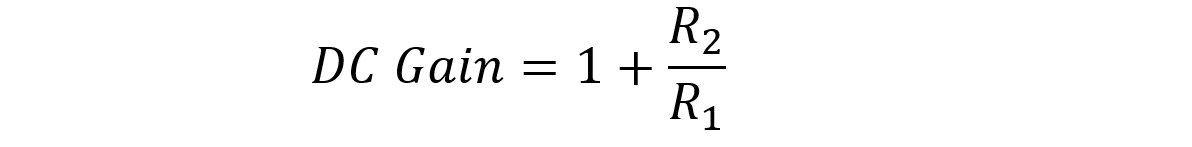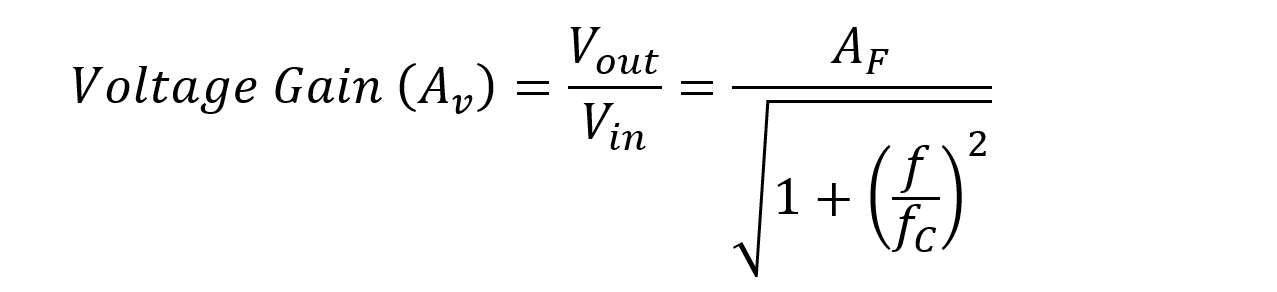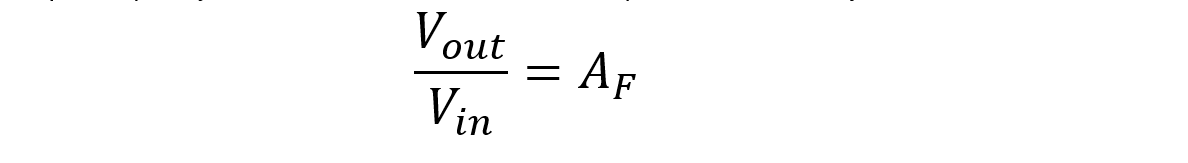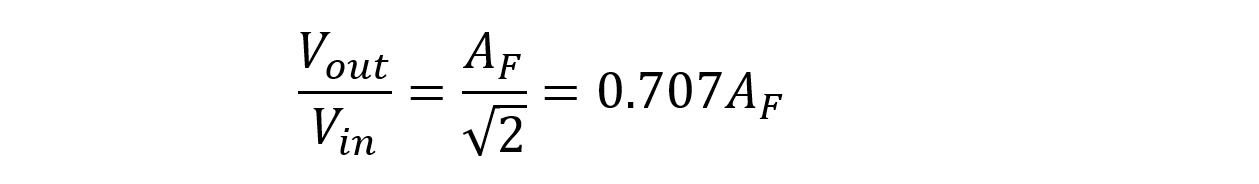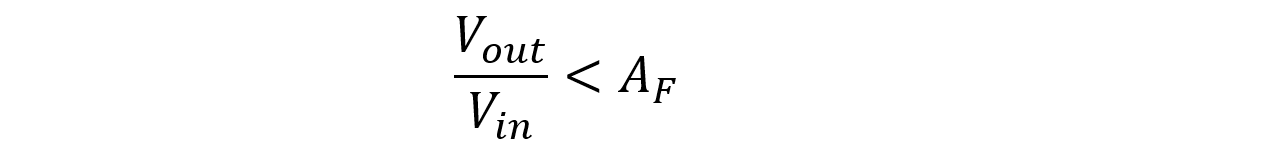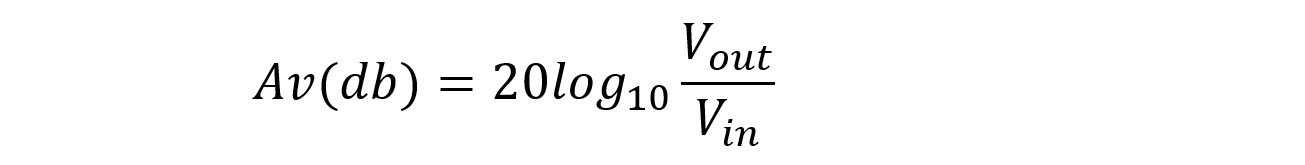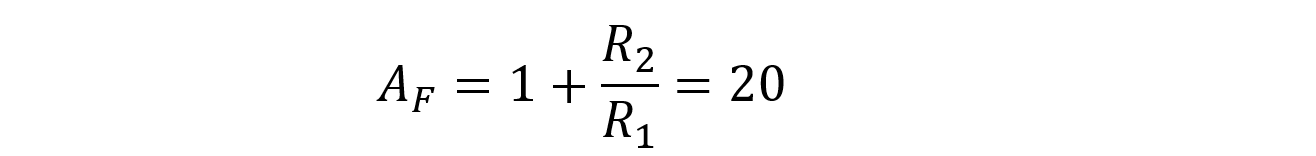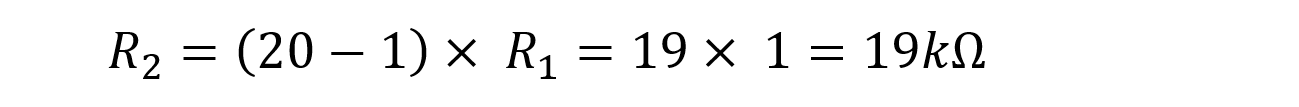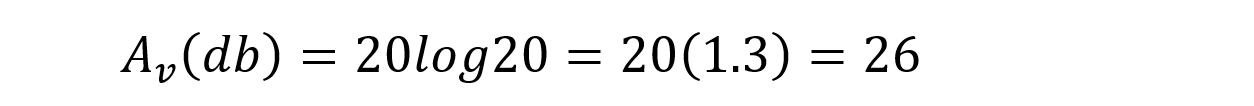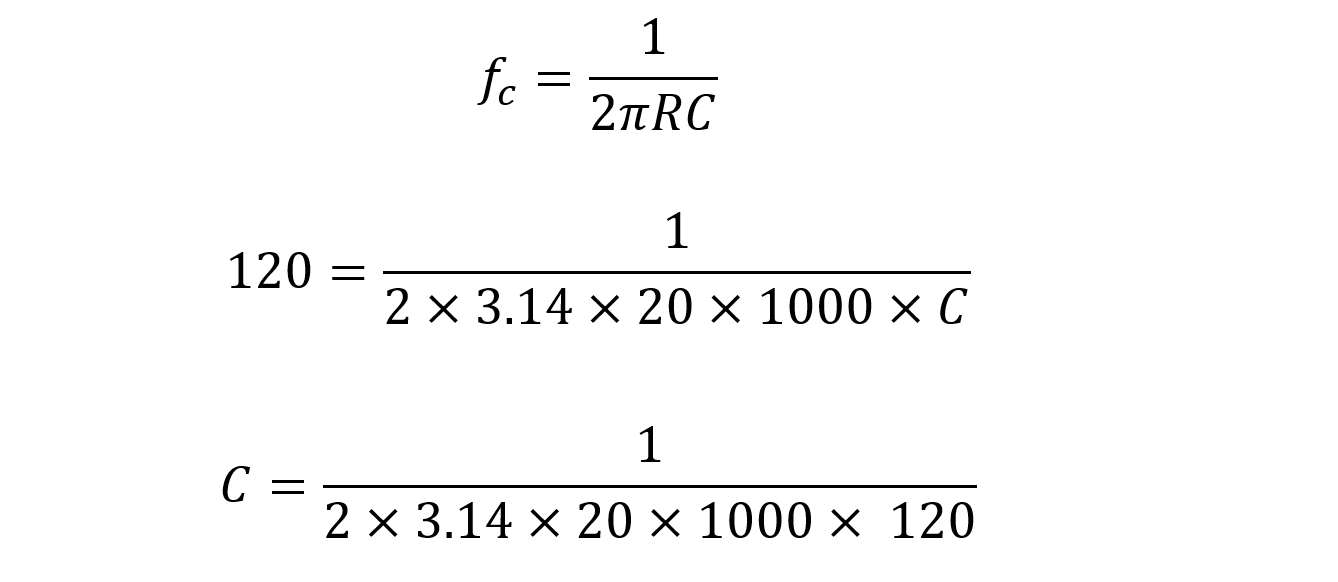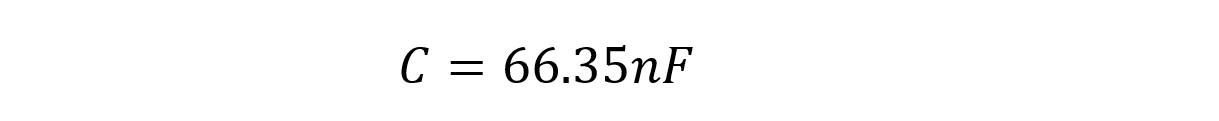Active filters employ op-amps to amplify the output signal. This article describes first order active low pass filters, non-inverting & inverting configurations with amplification circuits, second order active low pass filters and examples.
First Order Active Low Pass Filter
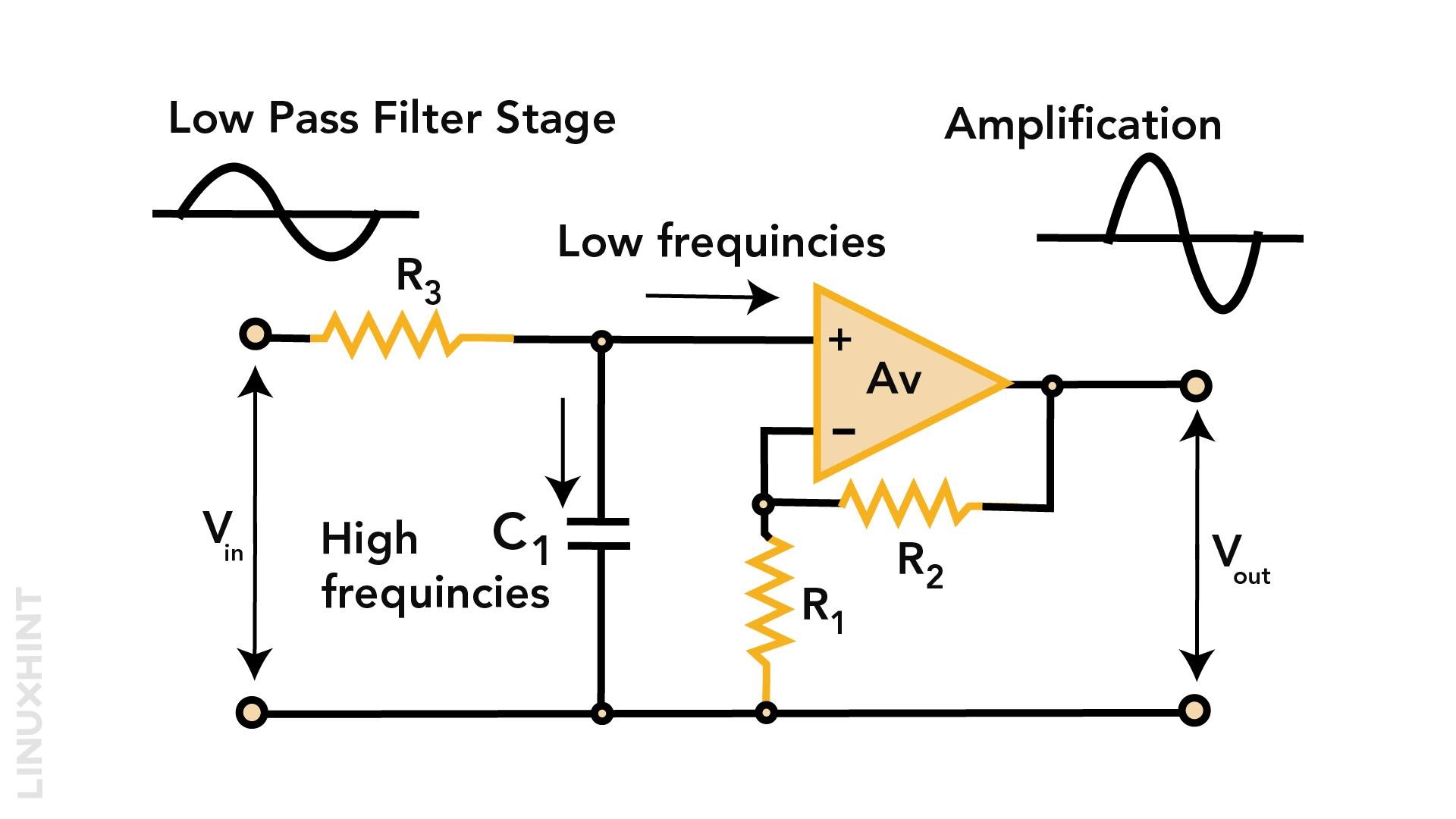
It is the basic configuration of an active low pass filter comprising RC filter with non-inverting operational amplifier. The DC gain is greater than the passive filter gain, whose gain is below unity.
Higher input impedance restricts excess load on filter output, while low output impedance prevents filter cut-off frequency to shift from original position due to change of impedance.
There is only one limitation with first order low pass filter configuration, which is a fixed voltage gain of 1. This filter cannot cross the unity voltage gain.
Low Pass Filter with Amplification
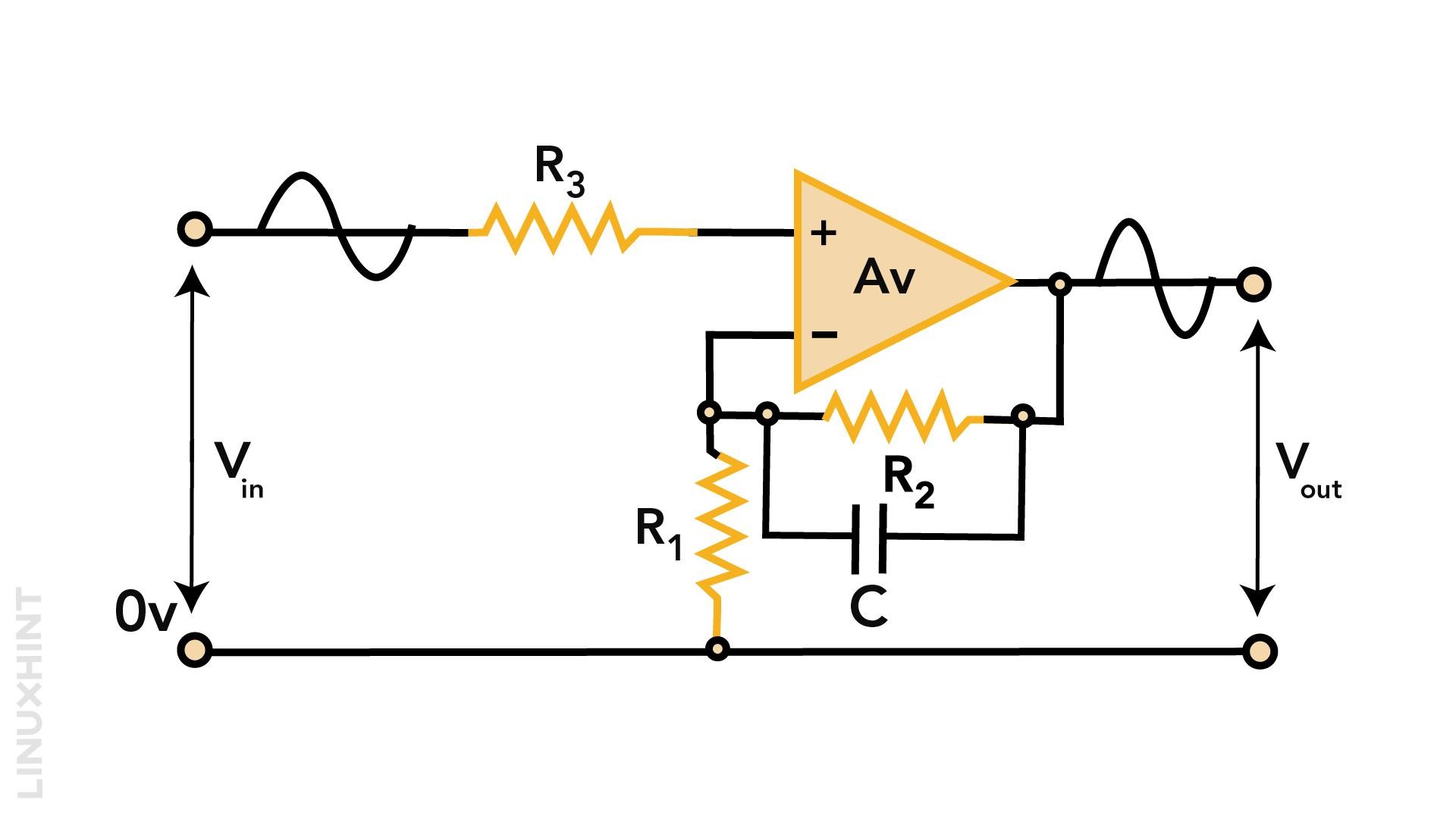
This configuration adds up feedback and input resistors at the inverting terminal of the op-amp and with the addition of resistors in the feedback loop, the voltage gain AF, above unity is achieved:
The dc voltage gain as function of feedback resistor and input resistor is expressed below:
Voltage Gain
We can also calculate gain of first order low pass filter in terms of frequencies:
Here AF is band pass gain, ‘f’ is input frequency & ‘fc’ is cut-off frequency.
We can get three verified states of operations of active low pass filter as described below:
1- At low frequencies f<fc
When input frequency is lower, f<fc, the above fraction equals numerator only.
2- At cut-off frequency f=fc
When input frequency equal cut-off frequency,
3- At high frequencies f>fc
When input frequency is greater than cut-off frequency,
Voltage gain may also be presented in decibels as:
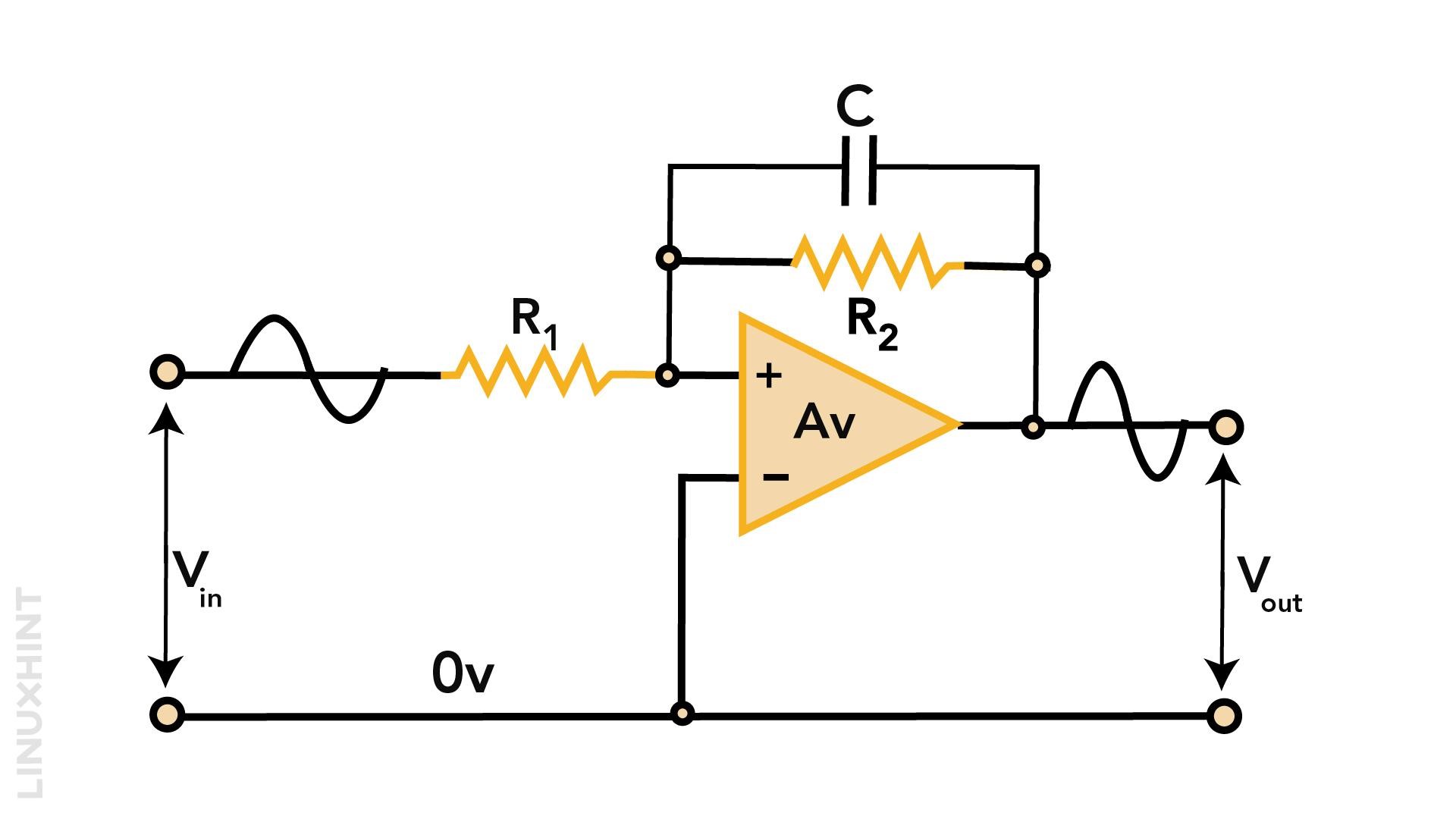
Inverting Amplifier Filter Circuit
The only limitation in first order low pass filters is displacement of cut-off frequencies from original position when there is change in input resistance value. This affects the performance of low pass filters. To avoid such an interference, an improved version of first order low pass filter with a capacitor in its feedback circuit is used. This arrangement bypasses resistor R2 while keeping a feedback loop for first order low pass filter.
Inverting amplifier filter circuits can set the cut-off frequency point to its original position. At low frequencies, Xc reaches very high values, while at high frequencies, Xc falls close to zero. The capacitor plays its role while it remains unaffected with any change in input resistance.
Non-Inverting Amplifier Filter Circuit
The input signal applies to non-inverting terminals in non-inverting amplifier filter circuit configuration. It also functions to position the cut-off frequency point at original position even if the external resistances change. However, the voltage gain in non-inverting amplifier filter circuit configuration is unity.
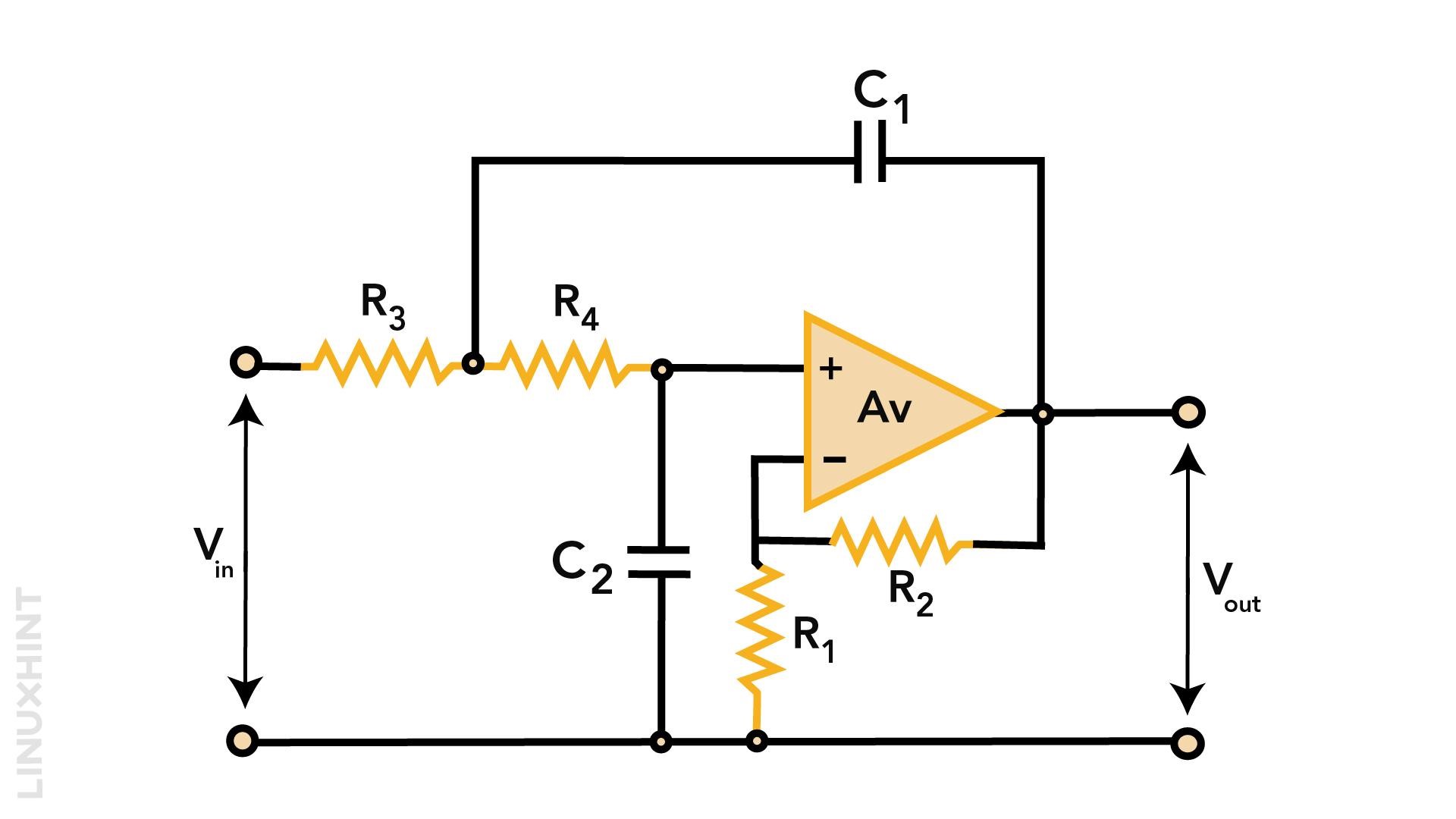
Second Order Active Low Pass Filter
A second order active low pass filter is obtained by replicating the RC network more than one time in circuit. The frequency response follows the same principle, except that the cut off-frequency point shall be shifted to the number of cascades of RC networks. For a second order filter, it means that the cut-off point shall be twice of 20db/decade. Moreover, the total voltage gain shall be the product of each individual gain.
Example
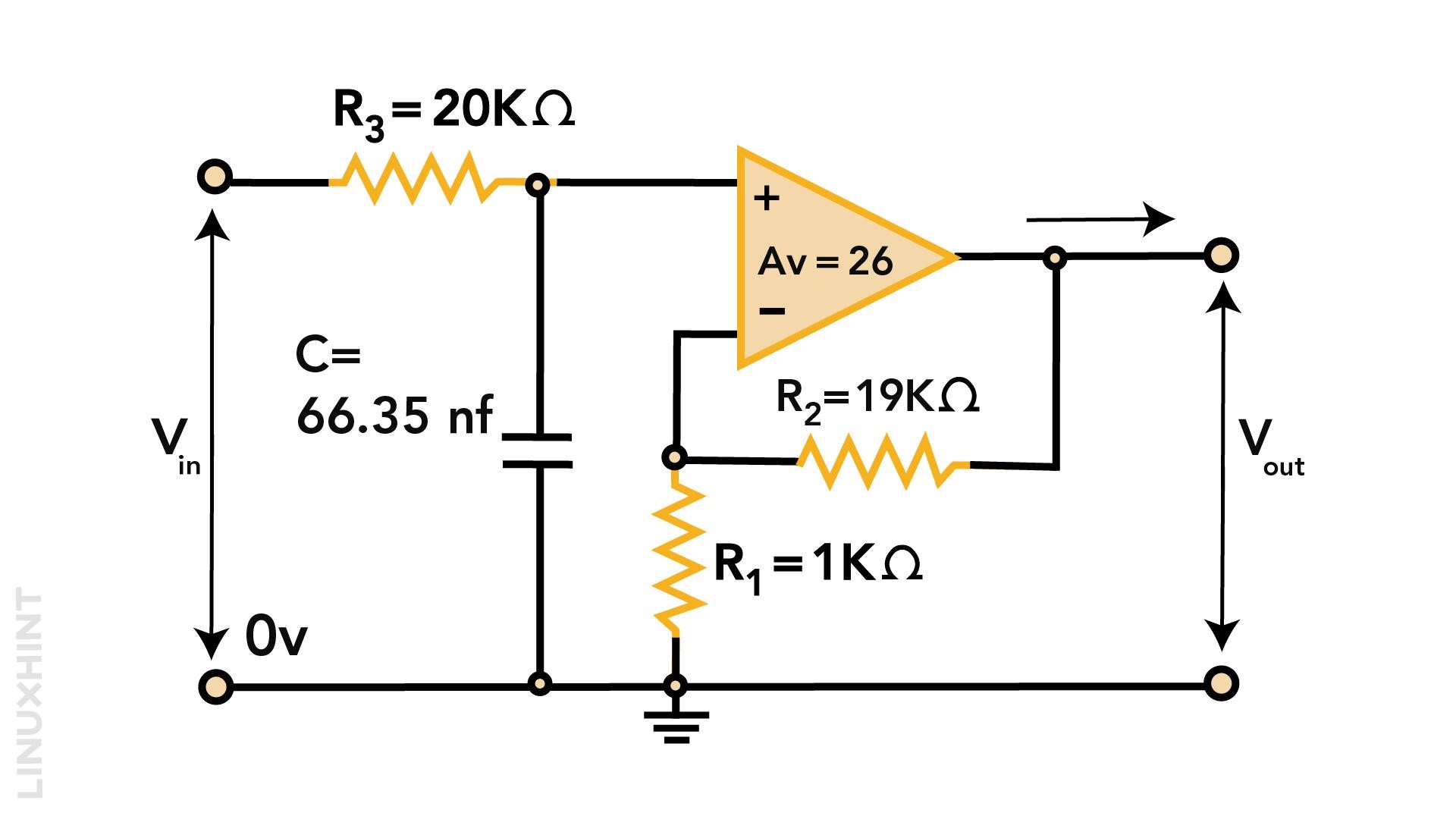
Calculate parameters of non-inverting low pass filter circuit with gain of 20 at low frequencies, cut off frequency 120Hz and input impedance 20KΩ.
The voltage gain of non-inverting amplifier is given by:
Assuming R1=1kΩ:
Voltage gain in decibels is given by:
The corner frequency is calculated as:
Hence, low pass filter can be designed as below:
Conclusion
Active low pass filters are combinations of passive low pass filters with operational amplifiers for amplification purposes. These filters have unity or higher gains with respect to low pass filters and therefore the output value does not attenuate due to passive components.