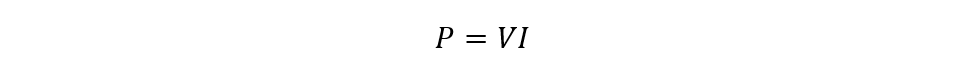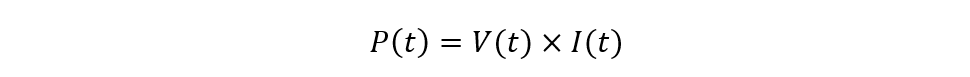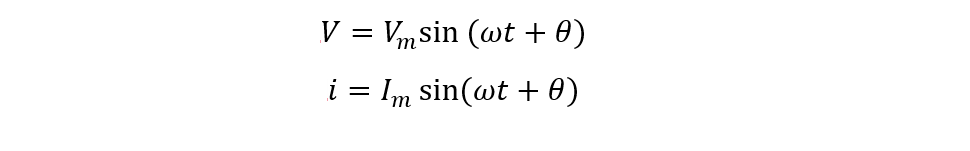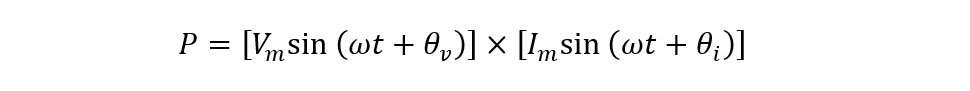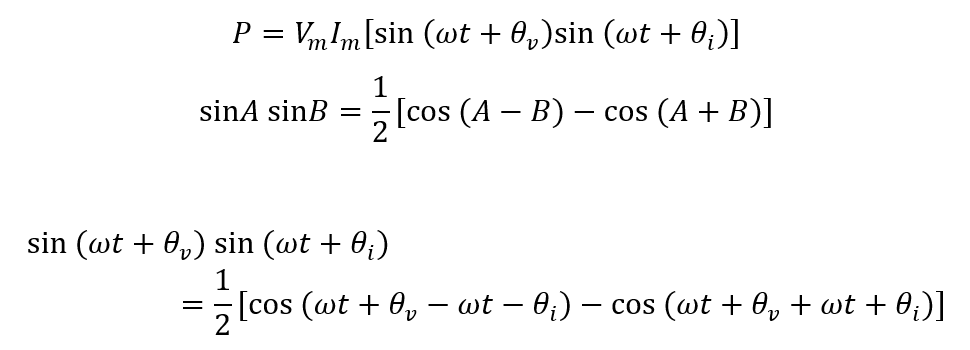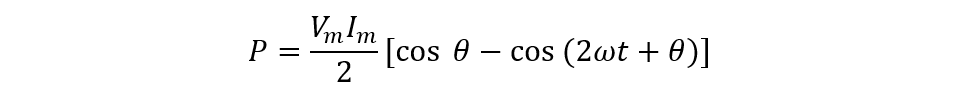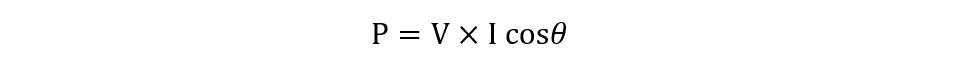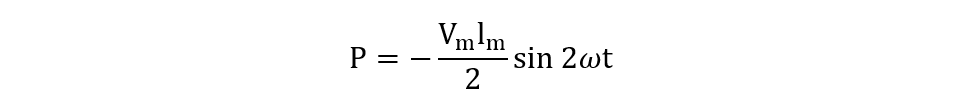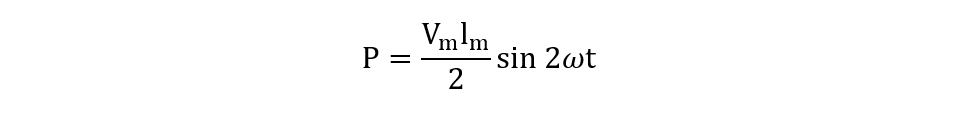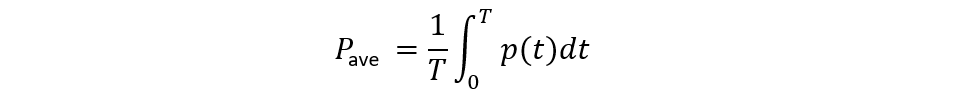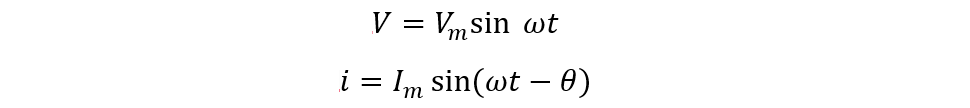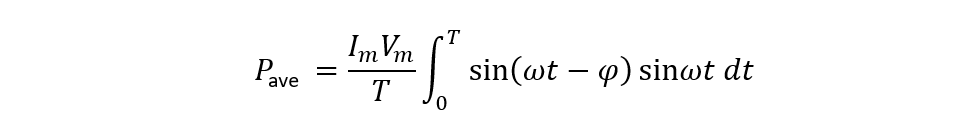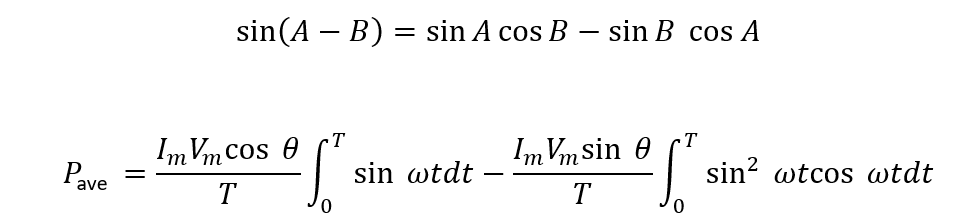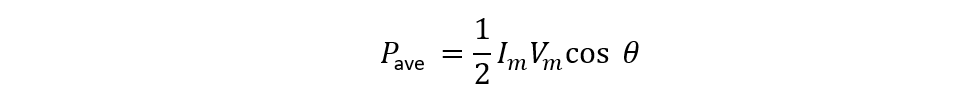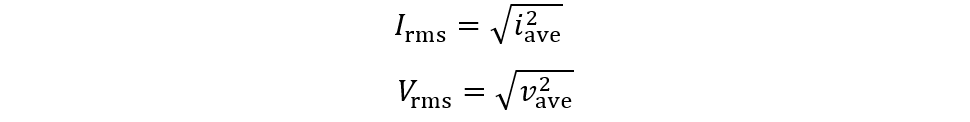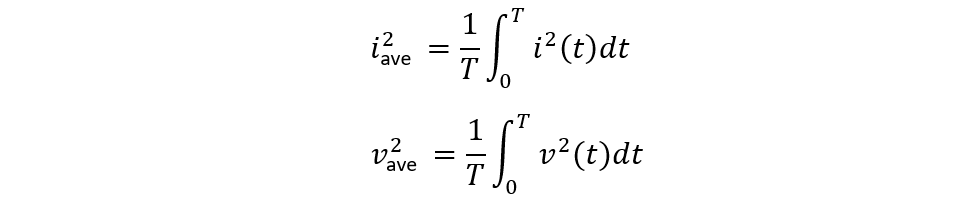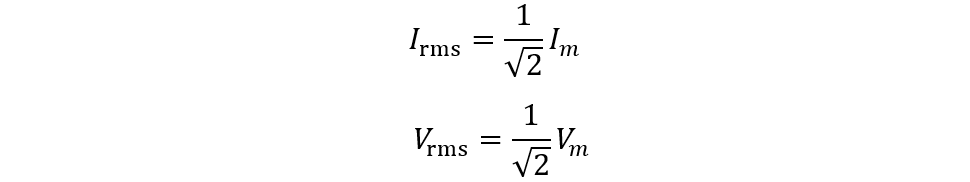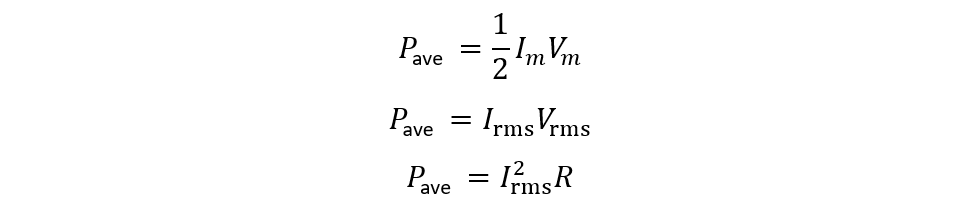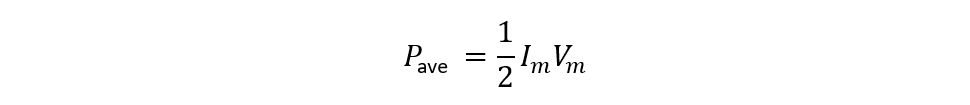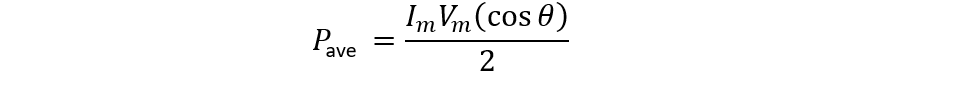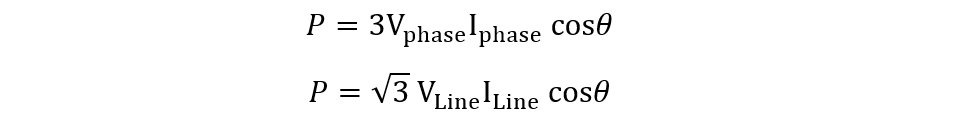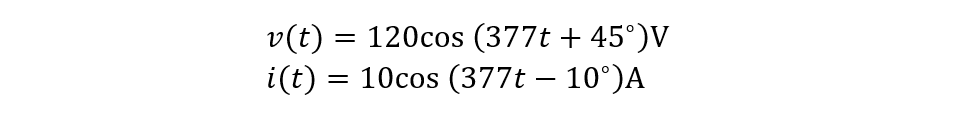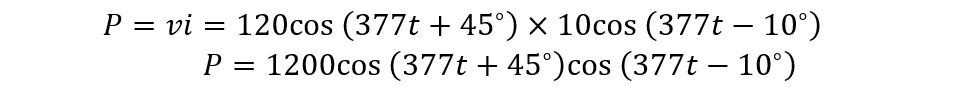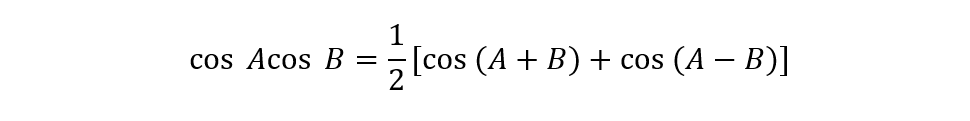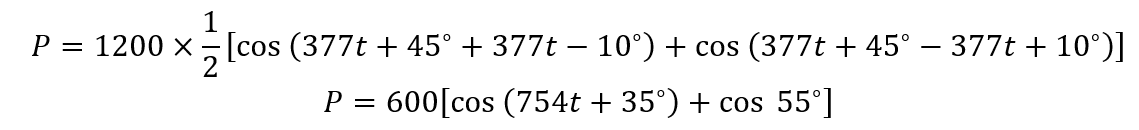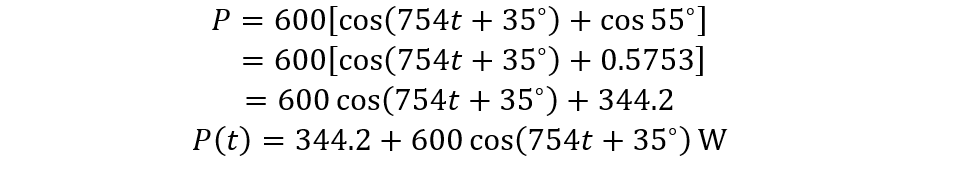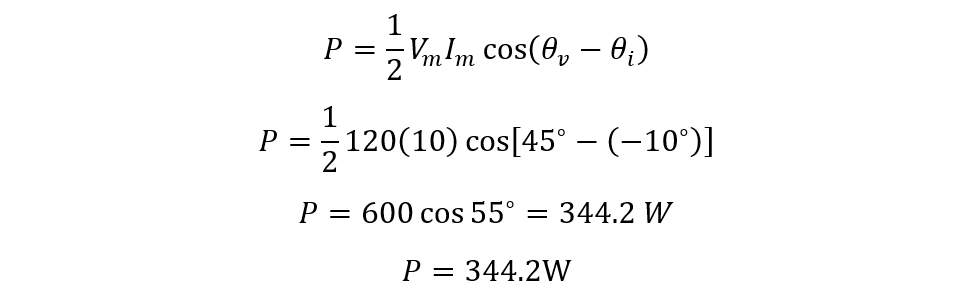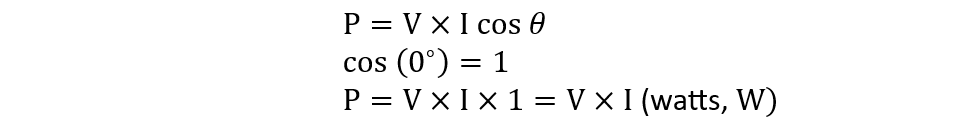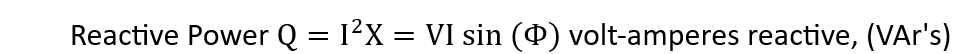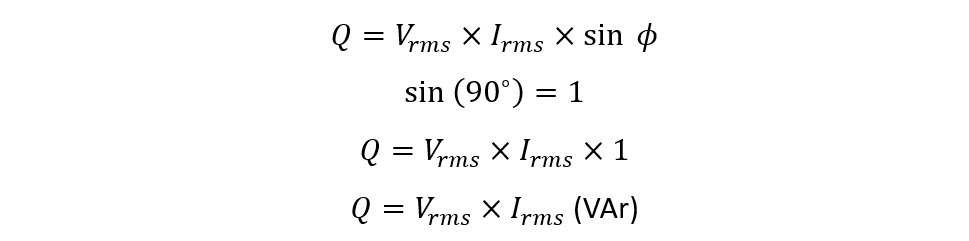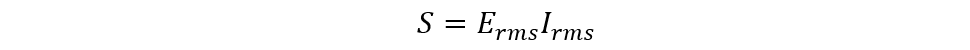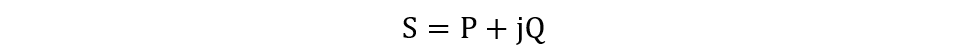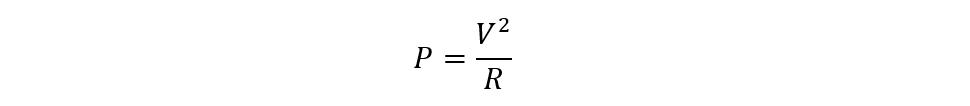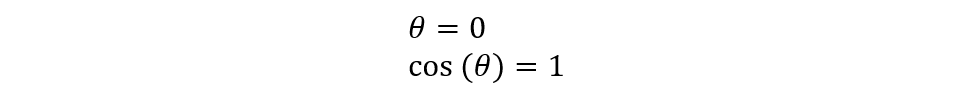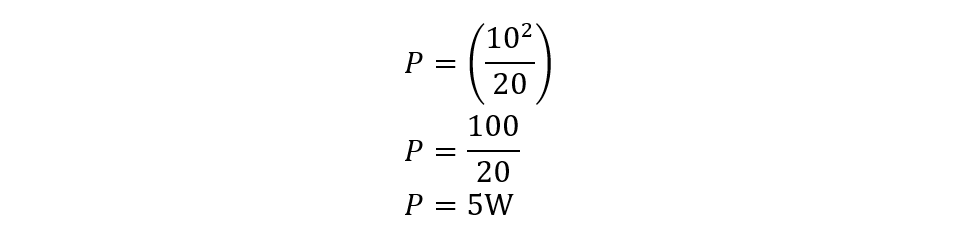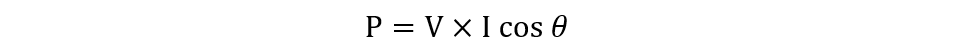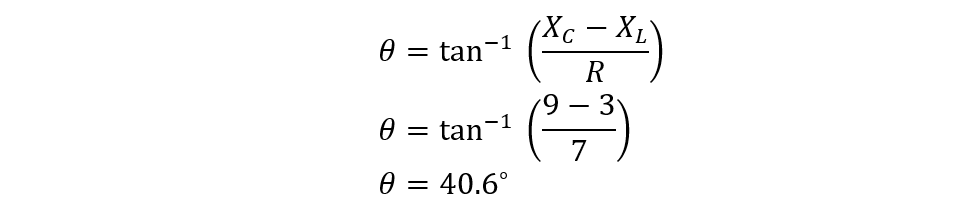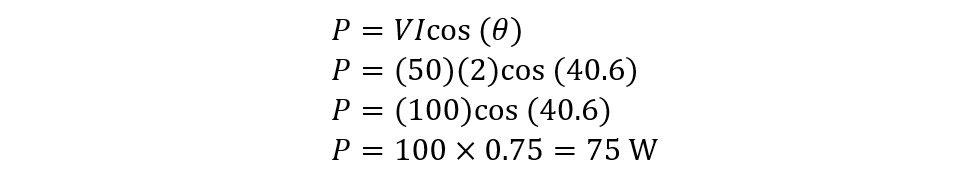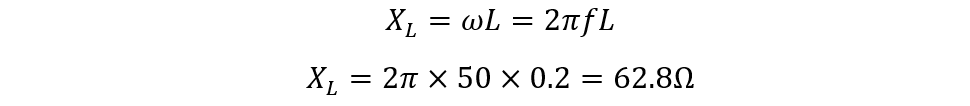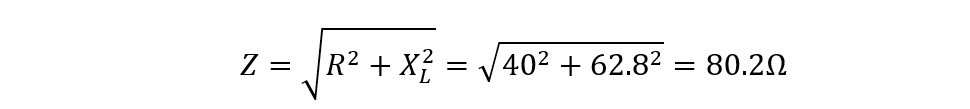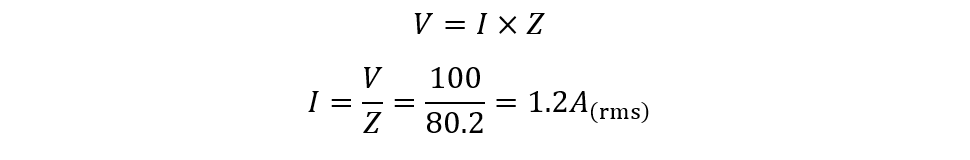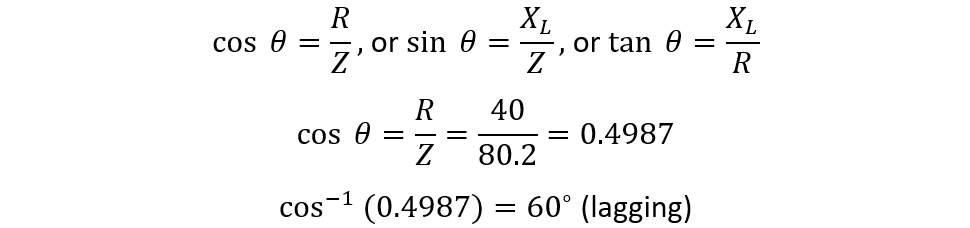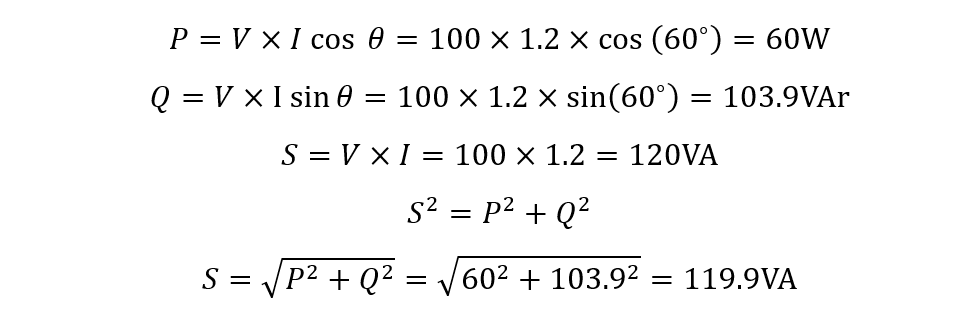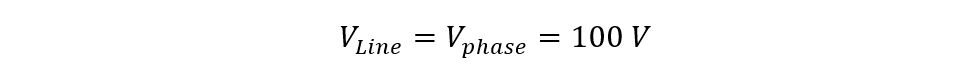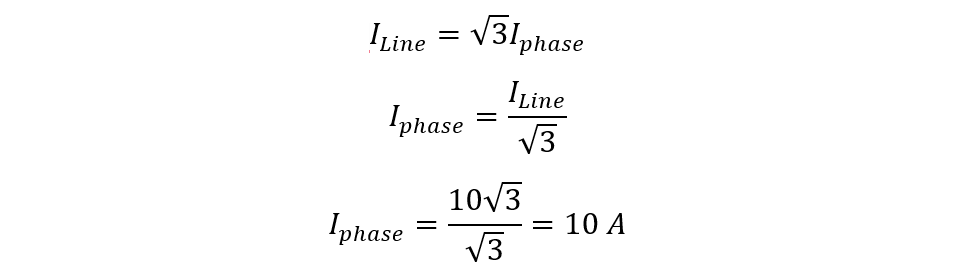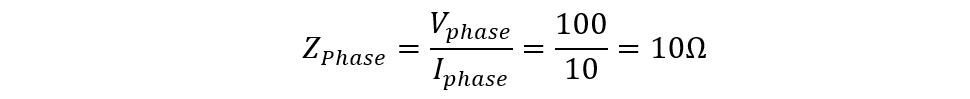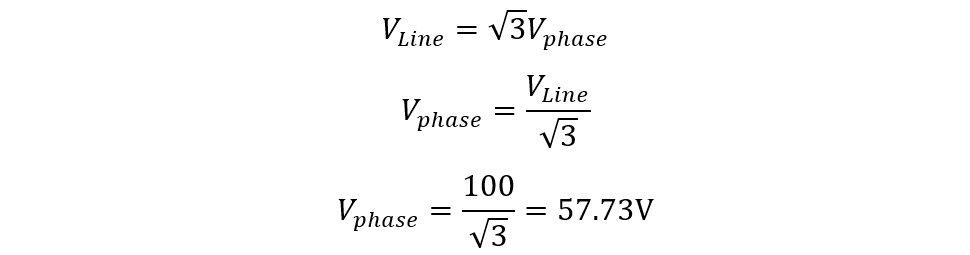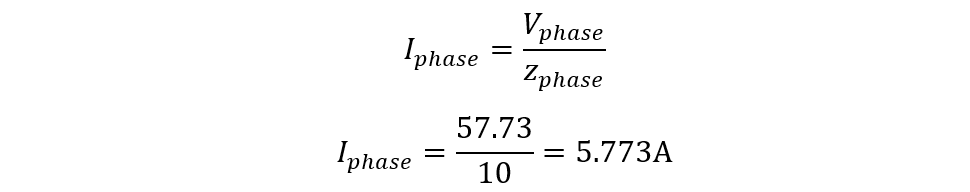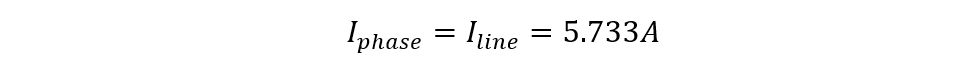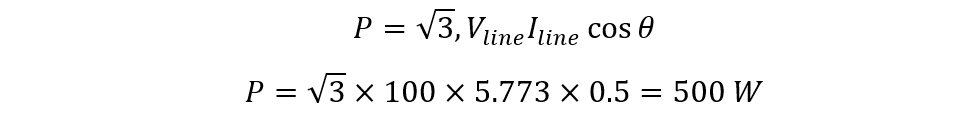Outline:
- Power in AC Circuits
- Instantaneous Power in AC Circuits
- Average Power in AC Circuits
- Types Of Power in AC Circuits
- Example 1
- Example 2
- Example 3
- Example 4
- Conclusion
Power in AC Circuits
The AC circuits having reactive components will have their voltage and current waveforms out of phase by some angle. If the phase difference between the voltage and current is 90 degrees, then the current and voltage product will have the same positive and negative values. The power consumed by the reactive components in AC circuits is nearly equal to zero, as it returns the same power that it consumes. The basic formula for calculating the power in an AC circuit is:
Instantaneous Power in AC Circuits
The instantaneous power is time-dependent and the voltage and current also depend on the time, so the basic formula for calculating power will be:
So, if the voltage and current are sinusoidal, then the equation for voltage and current will be:
So now placing the values for the current and voltage in the basic power formula, we get:
Now simplify the equation and use the below trigonometric formula:
Here, the ΦV is the phase angle of voltage and Φi is the phase angle of the current, the result of their addition and subtraction will be Φ so the equation can be written as:
Since the instantaneous power varies continuously with respect to the sinusoidal waveform, it can make the power calculation complex. The above equation can be made simpler if the number of cycles is fixed and the circuit is purely resistive:
In the case of purely inductive circuits, the equation for the instantaneous power will be:
In the case of purely capacitive circuits, the equation for the instantaneous power will be:
Average Power in AC Circuits
Since instantaneous power has continuously varying magnitude, it does not hold practical importance. The average power remains the same and does not vary with time, the average value of the power waveform remains the same. The average power is defined as the instantaneous power over one cycle, which can be written as:
Here T is the oscillation time period, and the equation for the sinusoidal voltage and current is:
Now the equation for the average power will become:
Now by using the trigonometric formula given below to simplify the average power equation:
After solving the above integration, we get the following equation:
Now to make the equation look like the DC counterpart the RMS values for the current and voyage are used and here is the equation for the RMS current and voltage:
Now as the definition of average power, the average voltage and current equations will be:
So now the RMS value for the voltage and current will be:
So now if the phase angle is zero degrees as in the case of the resistor, then the average power will be:
Now it is to be taken into account that the average power of the inductor and capacitor is zero but in the case of the resistor it will be:
In the case of the source, it will be:
In the three-phase balanced system, the average power will be:
Example: Calculating the Instantaneous Power and Average power of an AC Circuit
Consider a passive linear network connected with a sinusoidal source having the following voltage and current equations:
i) Find the Instantaneous Power
Putting the values of voltage and current in the power equation, we get:
Now use the following trigonometry formula to simplify the equation:
So, the instantaneous power will be:
Now further solving the by finding cos 55 we get:
ii) Finding the Average Power of the Circuit.
Here the value of the voltage is 120 and the current has the value of 10, further the angle for voltage is 45 degrees, and for current the angle is 10 degrees. So now the average power will be:
Types Of Power in AC Circuits
In AC circuits, the type of power mainly depends on the nature of the load connected, the power supply can be either single-phase or three-phase. So, the power in an AC circuit can be classified into the following types:
- Active Power
- Reactive Power
- Apparent Power
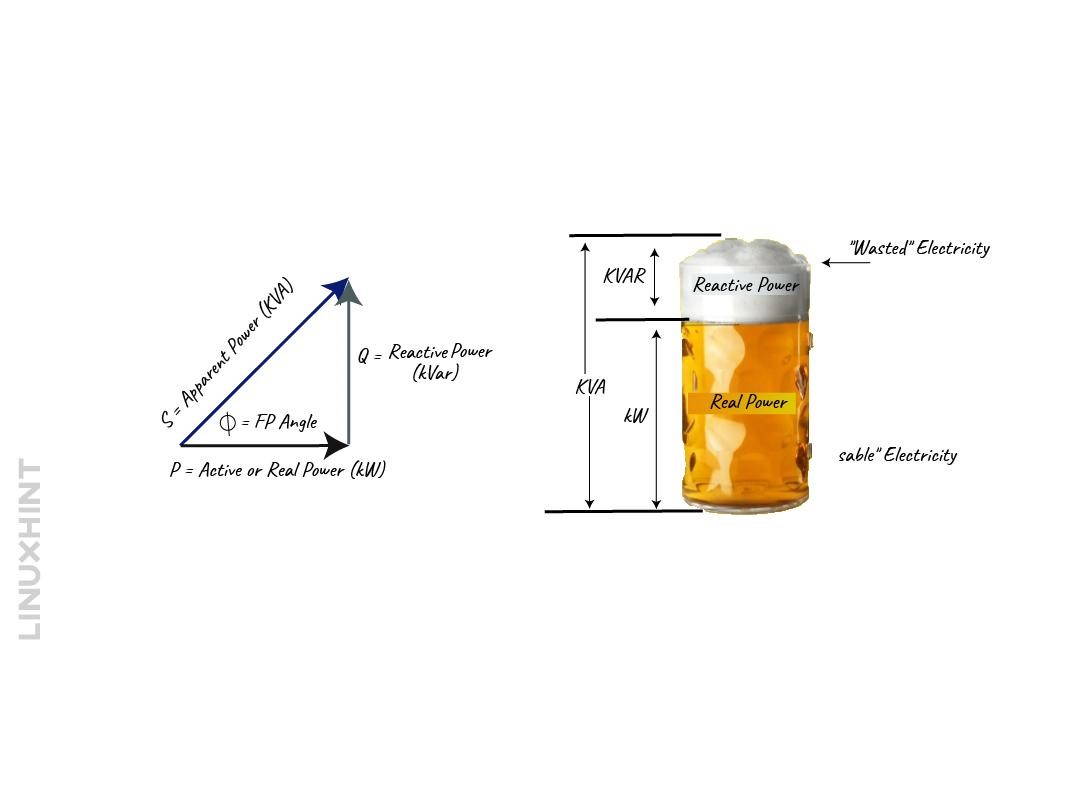
Further to get an idea of these three types of power below is the image that clearly describes each type:
Active Power
As from the name, the actual power that carries out the work is referred to as the real power or the active power. Unlike DC circuits, AC circuits always have some phase angle between the voltage and the current, except in the case of resistive circuits. In the case of a pure resistive circuit, the angle will be zero and the cosine of zero is one of the equations for the active power will:
Reactive Power
The power that is consumed in an AC circuit but does not perform any work like real power is referred to as reactive power. This type of power is usually in the case of inductors and capacitors and greatly impacts the phase angle between the voltage and current.
Due to the creation and reduction of the capacitor electric field and the magnetic field of the inductor, this power takes away the power from the circuit. In other words, it is produced by the reactance of the circuit’s reactive components, below is the equation for finding the reactive power in an AC circuit:
The reactive components in the circuit usually have voltage and current phase difference of 90 degrees, so now if the phase angle between the voltage and current is 90 degrees then:
Apparent Power
The apparent power is the total power of the circuit that consists of both the real and reactive power or to put it differently, it is the total power provided by the source. So, the apparent power can be written as the product of RMS values of current and voltage, and the equation can be written as:
There is another way of writing an equation for the apparent power, and that is the phaser sum of the active and reactive power:
Apparent power is normally used to express the rating of the devices that are used as sources of power, like generators and transformers.
Example 1: Calculating the Power Dissipation in Circuit
Consider a purely resistive circuit having an RMS value of resistance of about 20 Ohms and an RMS value of voltage, of about 10 Volts. To calculate the power dissipated in the circuit, use:
As the circuit is resistive so the voltage and the current will be in phase so:
Now put the values in the formula:
The power dissipated in the circuit is 5 W.
Example 2: Calculating the Power of an RLC Circuit
Consider an RLC circuit connected to a sinusoidal voltage source having an inductive reactance of 3 Ohms, Capacitive reactance of 9 Ohms, and a resistance of 7 Ohms. If the RMS value of current is 2 Amps and the RMS value of voltage is 50 Volts, then find the power.
The average power equation is:
To calculate the angle between the voltage and current using the following equation:
Now placing the values in the equation for the average power, we get:
Example 3: Calculating the Real, Reactive, and Apparent power of an AC Circuit
Consider an RL circuit connected with sinusoidal voltage and having an inductor and resistor connected in series. The inductor has an inductance of 200mH, and the resistance of the resistor is 40 Ohms, the supply voltage is 100 volts with a frequency of 50 Hz. Find the following:
i) Impedance of the circuit
ii) Current in the circuit
iii) Power factor and Phase Angle
iii) Apparent Power
i) Finding the Impedance of the circuit
For impedance calculation, calculate the inductive reactance of the inductor and for that use the given values of inductance and frequency:
Now find the impedance of the circuit using:
ii) Finding the Current in the Circuit
To find the current in the circuit using the Ohm’s law:
iii) Phase Angle
Now, finding the phase angle between the voltage and current:
iii) Apparent Power
To find the apparent power, the real and reactive power values should be known so first finding the real and apparent power:
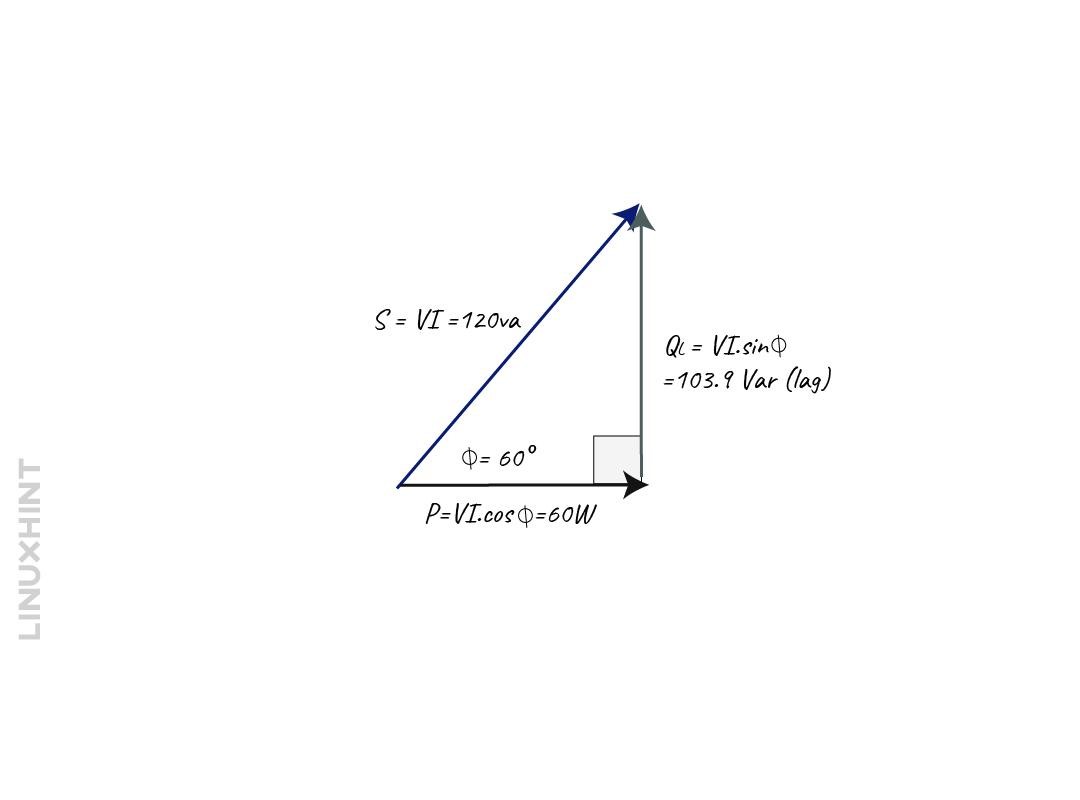
Since all the values are calculated, the power triangle for this circuit will be:
To more about the power triangle and power factor, read this guide.
Example 4: Calculating the Power of a Three-Phase AC Circuit
Consider a three-phase delta-connected circuit having three coils having a line current of 17.32 Amps at the 0.5 power factor. The line voltage is 100 volts, calculate the line current and total power if the coils are connected in a star configuration.
i) For Delta Configuration
The given line voltage is 100 Volts, in this case, the phase voltage will also be 100 Volts, so we can write:
However, the line current and phase current in the delta configuration is different, so use the line current equation to calculate the phase current:
Now we can find the phase impedance of the circuit using the phase voltage and phase current:
ii) For Star Configuration
Since the phase voltage is 100 volts, the line current in the star configuration will be:
In the star configuration, the line voltage and phase voltage are the same so calculating the phase voltage:
So now the phase current will be:
iii) Total Power in a Star Configuration
Now we have calculated the line current and line voltage in the star configuration, the power can be calculated using:
Conclusion
In AC circuits, power is the measure of the rate at which the work is being done, or to put it differently it is the total energy that is transferred to the circuits with respect to time. The power in an AC circuit is further divided into three parts and those are real, reactive, and apparent power.
Real power is the actual power that does the work, whereas the power that flows between the source and the circuit’s reactive components is the reactive power and is often referred to as unused power. The apparent power is the summation of real and reactive power, it can also be referred to as total power.
The power in an AC circuit can be measured either as instantaneous power or average power. In capacitive and inductive circuits, the average power is zero, as in an AC circuit the average power is nearly the same throughout the circuit. The instantaneous power on the other hand is dependent on time, so it is continuously varying.