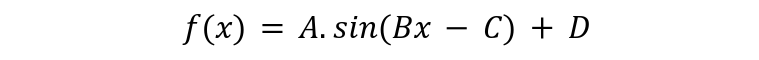What is Phase?
Phase represents the angle of the alternating signal. An alternating signal shifts its phase from 0°, 90°, 180 °, 270 ° and 360 °. Usually, radians are opted to represent angles of an alternating quantity. Therefore, alternating signals phases will be represented by 0, π/2, π, 3π/2 and 2π as shown below:
 What is the Phase Difference?
What is the Phase Difference?
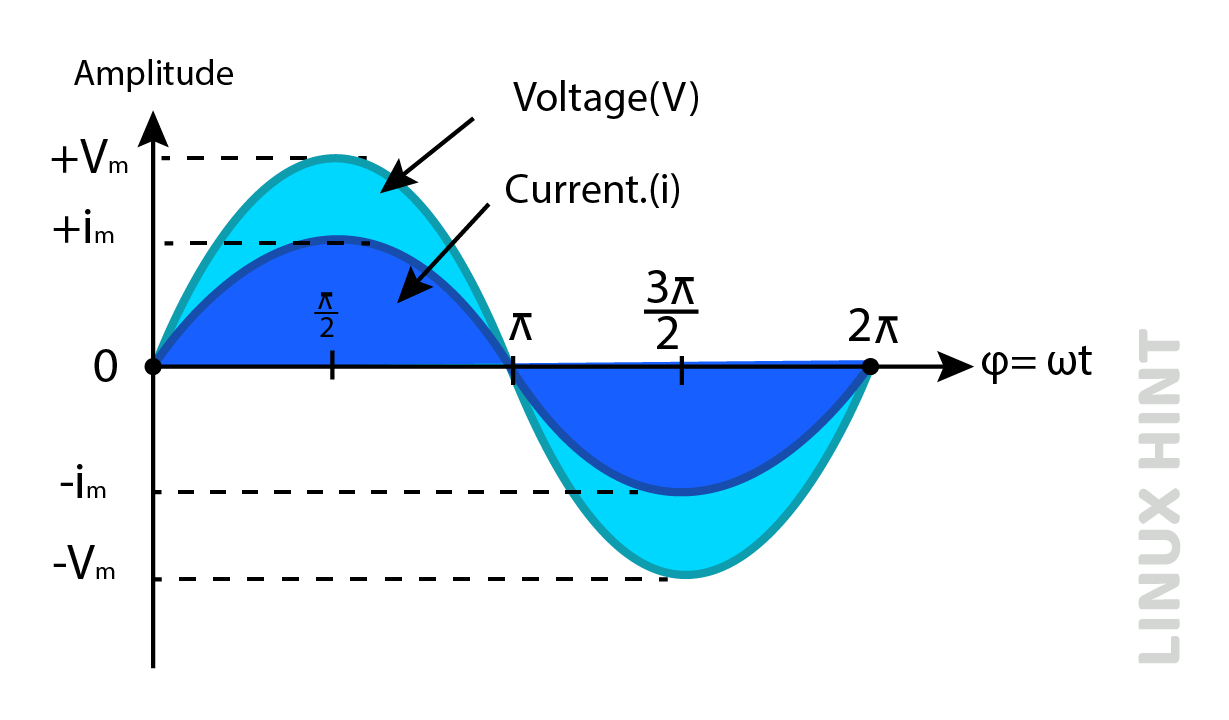
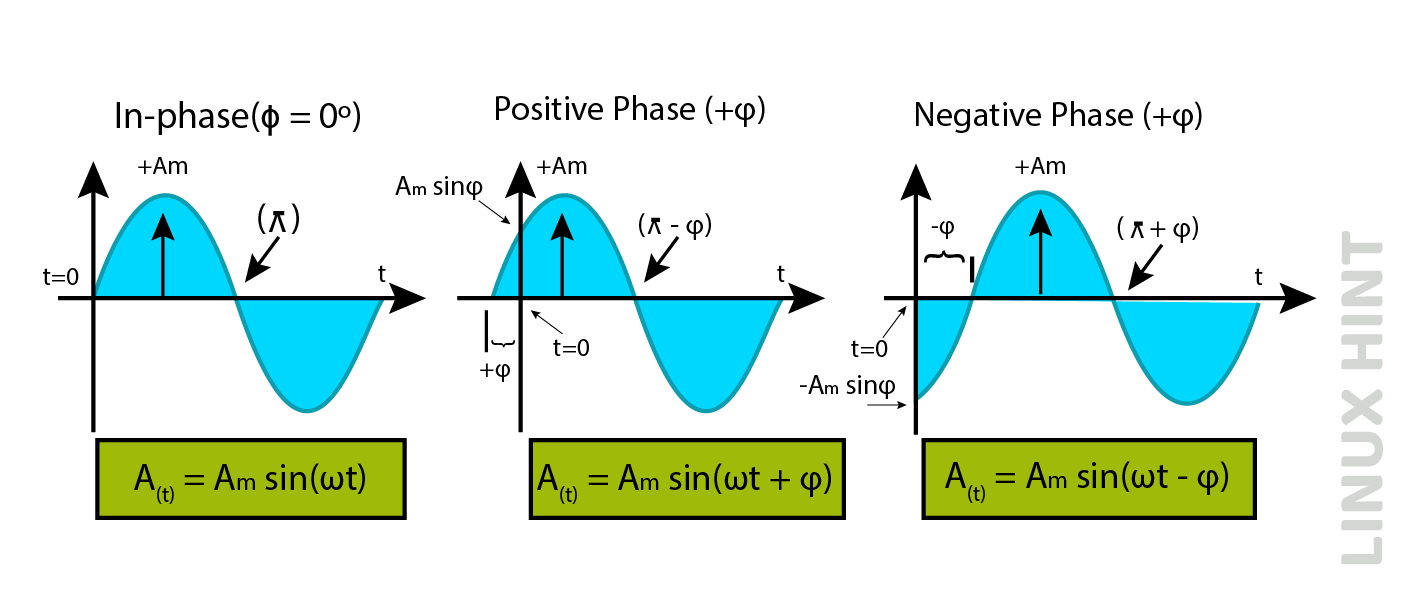
If two alternating signals pass through 0, π/2, 3π/2 and 2π at the same instance, there is no phase difference and phase shift is zero in this case. This case occurs in similar frequency signals, and such quantities with no phase difference are said to be in-phase with each other. The example of in-phase alternating quantities is shown below:
Consider another case of two alternating quantities that do not pass between maximum and zero values at the same instant, as shown below. The two alternating quantities display a phase delay between them. We can say that one alternating quantity leads to the other.
The phase difference between two alternating quantities is angle φ and the phase shift of the first alternating quantity (denoted by blue line) in this case, is its phase plus the addition of phase difference of φ. We can say that the first alternating quantity shows a phase shift of φ from the other one.
Mathematical Expression
The standard equation for AC quantities is presented as:
Here, φ represents the phase of the alternating quantity. The values of φ can be both positive and negative, therefore ± is indicated with phase. Am is amplitude and ωt is angular frequency of an alternating signal.
If the phase shift of the wave is exactly 90 degrees with the reference origin point, then the waveform is called cosine wave. A cosine wave is just like a sine wave whose phase shift is exactly 90 degrees or π/2 radians. The expression of cosine wave is therefore:
Example: Calculating the Phase Difference
If x = asin(ωt+π/3) and y= acosωt ,calculate phase difference for this case for the two waves.
As:
Obtaining phase from the first wave expression:
Now, second wave is given as:
For obtaining phase from the second wave expression, we can convert the cosine wave into its equivalent sine wave:
Now, phase can be obtained as:
Phase difference is difference of the two waves phases:
Phase Shift
Phase shift occurs when either the graph of sine function or cosine function of a signal shifts itself to left or right from their usual position. The phase shift is usually represented by an additional angle in the sine or cosine functions. There can be three different scenarios of phase shifts: zero, positive or negative phase shifts.
Mathematical Expression
The phase shift equation is presented in sine function as:
The phase shift equation is presented in cosine function as:
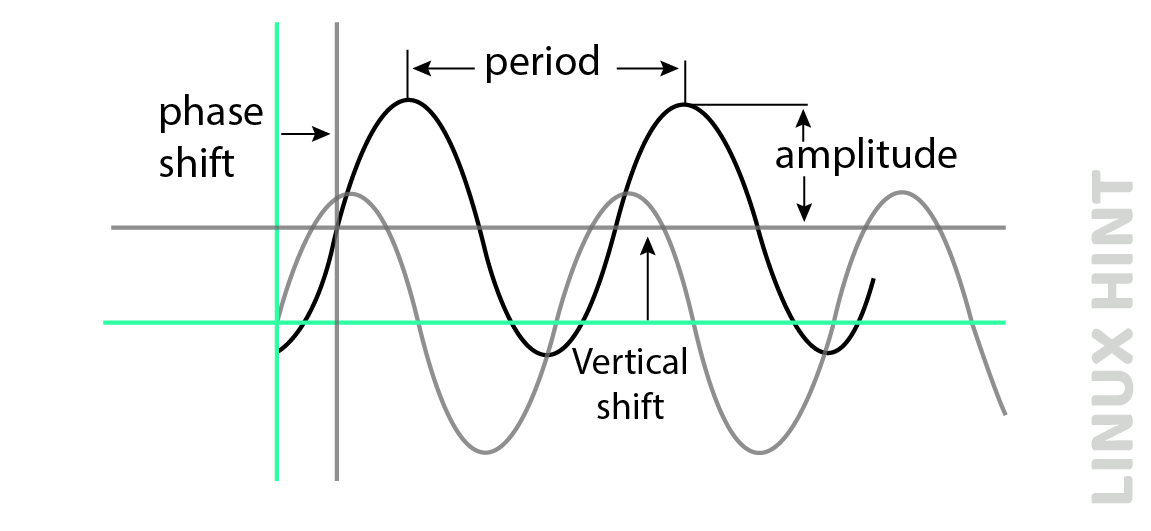
The four numbers expressed as A, B, C and D in the above expressions provide values of four parameters. ‘A’ represents amplitude of wave, ‘B’ represents its period while ‘C’ represents its horizontal phase shift and ‘D’ represents its vertical phase shift.
For period calculation, the expression of 2π/B is used and for phase shift, the expression of C/B is used. Values of ‘A’ and ‘D’ are extracted without any change.
Zero, Positive & Negative Phase Shift
The positive and negative phase shift can be described in terms of phase shift of AC signals with different values of phase angles. The cases of zero, positive & negative phase shift are presented below:
In case of zero phase shift, when phase angle is ‘0’, the alternating signal starts at t=0 as shown for the in-phase case above. So φ=0 and equation for AC waveform becomes as below:
In case of positive phase shift, when phase angle is ‘0’, the alternating signal starts before the reference or origin point right before t=0. This depicts that the phase of the alternating signal is in lead from the reference point and φ is positive. So, AC waveforms follows:
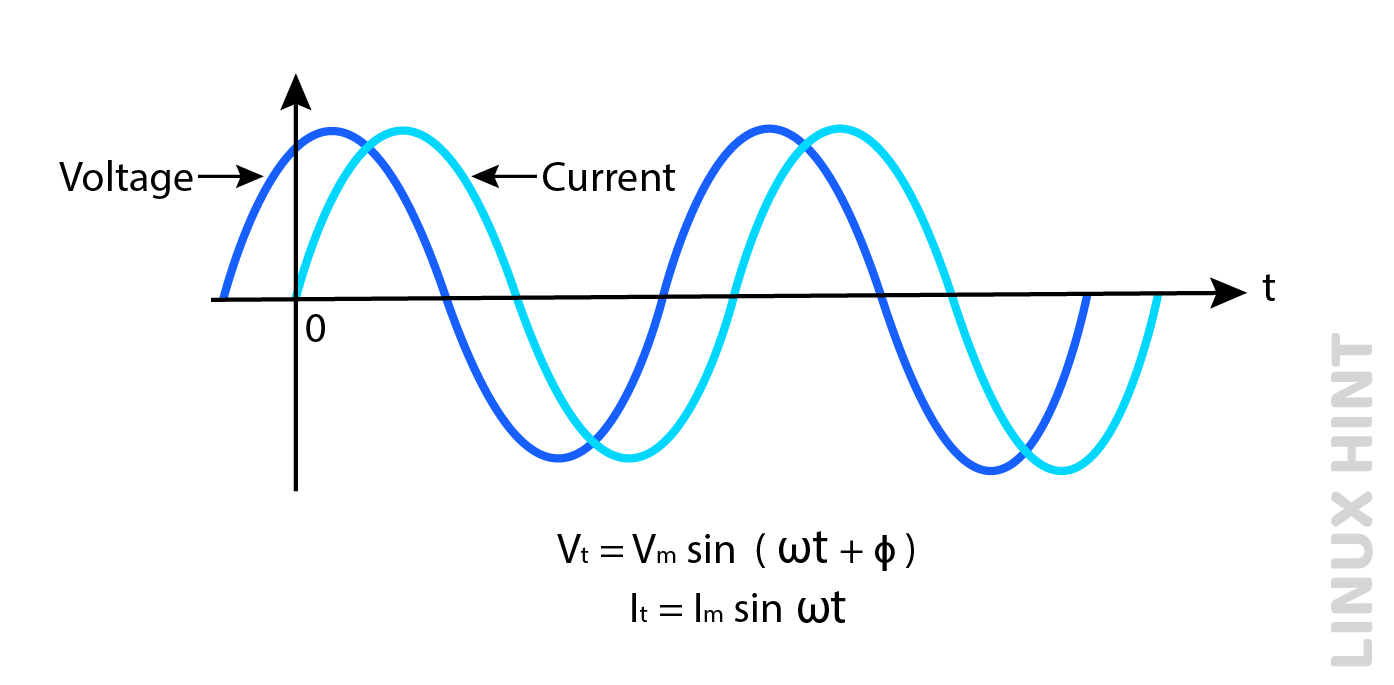
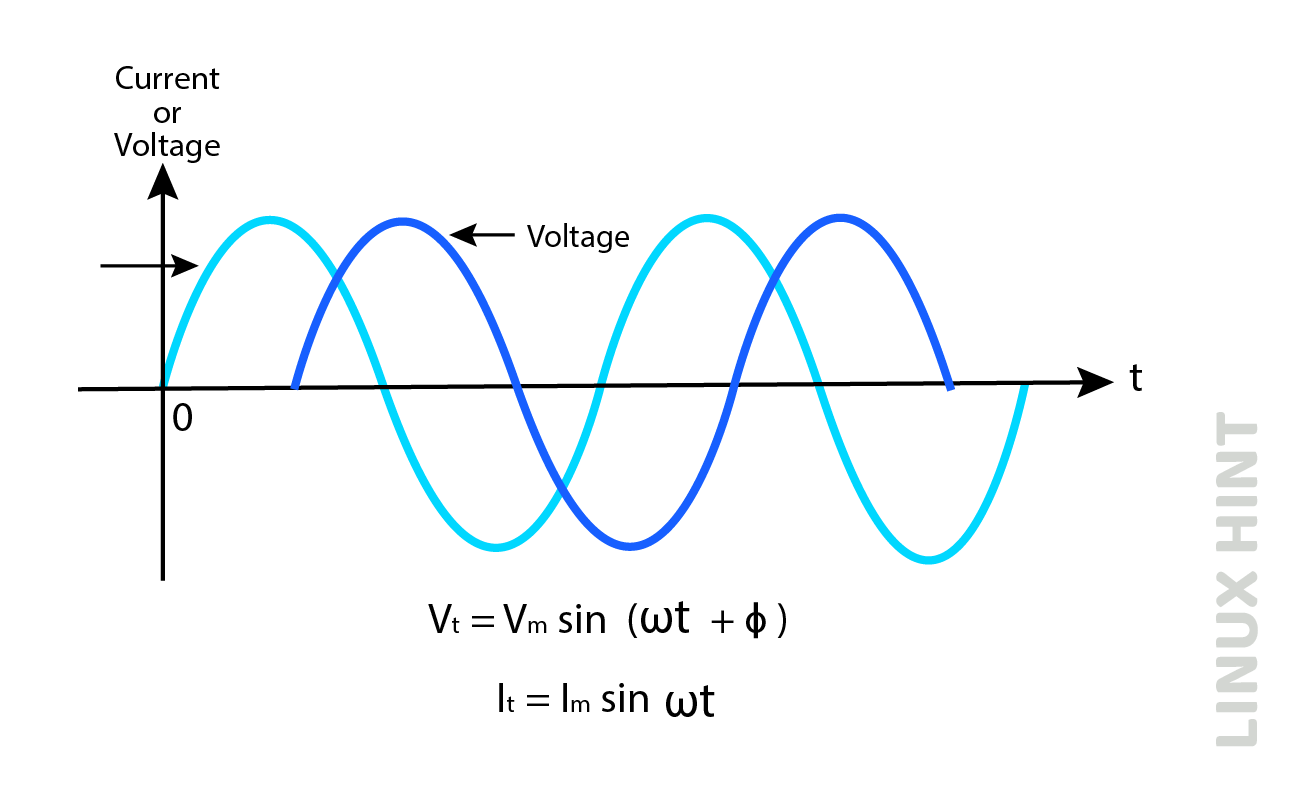
The positive phase case can be understood through examples of inductors. In inductors, voltage leads to current. So, by above demonstration, the voltage waveform shall start from the left of origin as shown below:
In case of negative phase shift, at phase angle of ‘0’, the alternating signal does not start right at the reference point but starts with a delay. The waveform will be represented shifted right to the reference point. Therefore, φ is negative and AC waveform is expressed as:
The negative phase delay case can be seen in the case of capacitors. In a capacitor, current leads to voltage. As voltage lags, it would be seen starting with delay or shifted towards right of origin as shown below:
 Example: Calculating the Phase Shift
Example: Calculating the Phase Shift
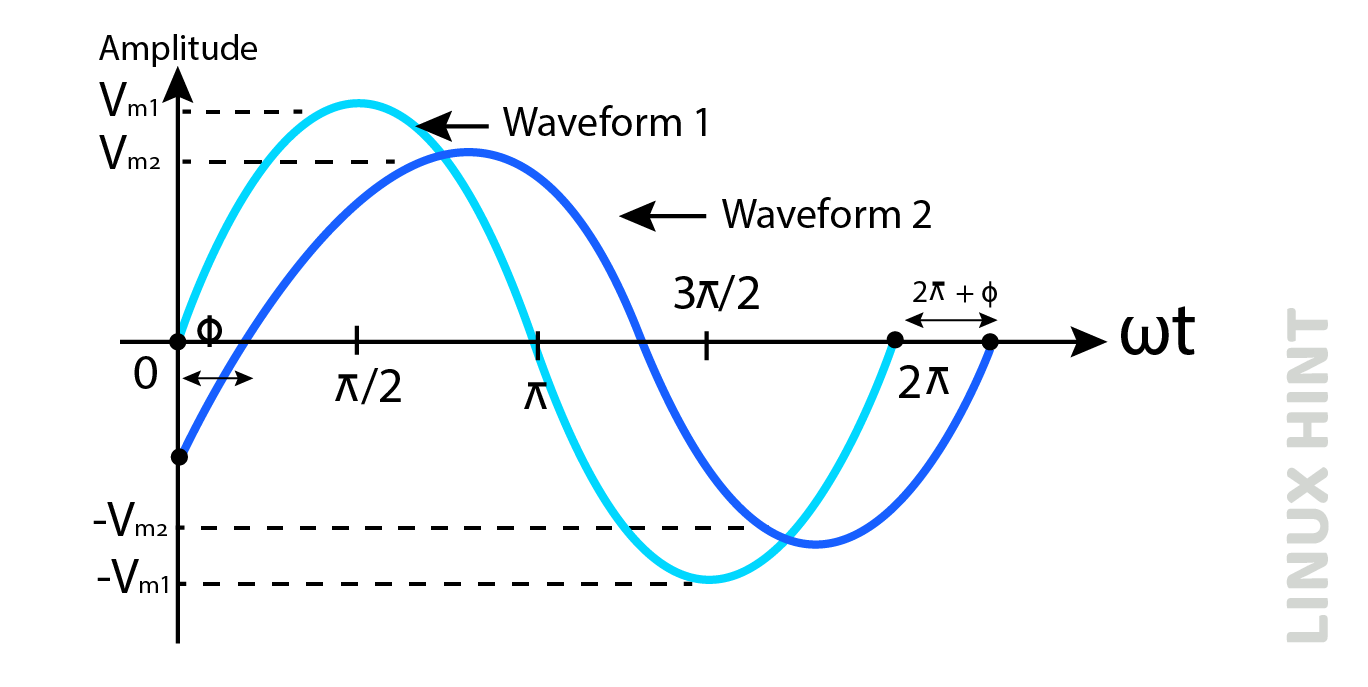
If f(x) = 1.5.sin(3x-4)+5, calculate the amplitude, time period, its phase shift and its vertical shift. Comparing the given function with standard phase shift equation:
We get followings:
Amplitude: A= 1.5
Period: 2π/B=2π/3
Phase Shift: C/B= 4/3
Vertical Shift: D=5
The phase shift value obtained above is positive. It means a positive phase shift and shift of the graph towards the left of the usual position.
Conclusion
Phase difference is the difference in terms of phase or angle between two alternating quantities. Based upon phase differences, alternating quantities can be said to be in-phase and out of phase. Phase shift is the value of measured phase difference in radians.

 What is the Phase Difference?
What is the Phase Difference?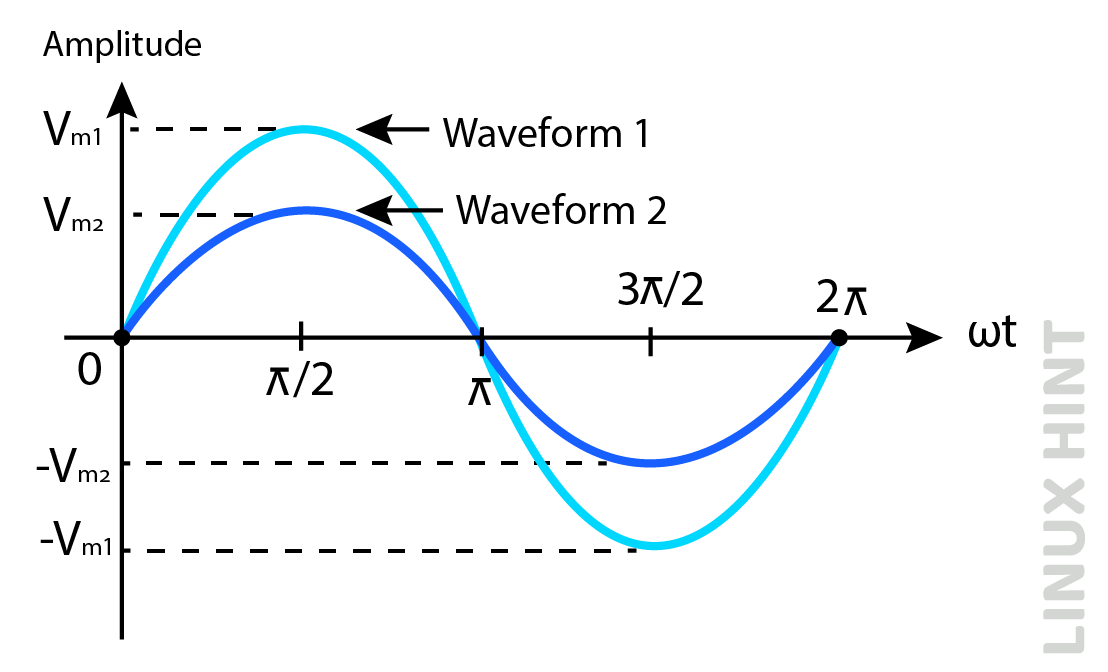
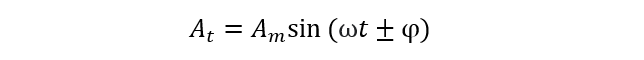
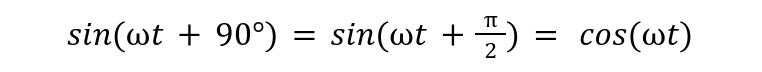
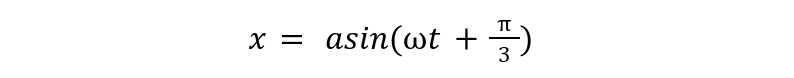
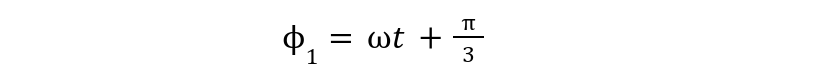
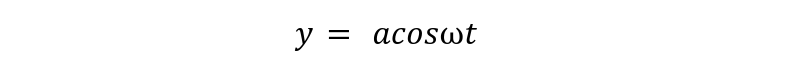
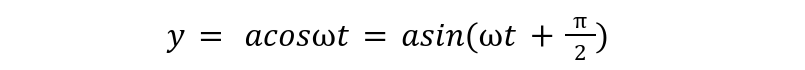
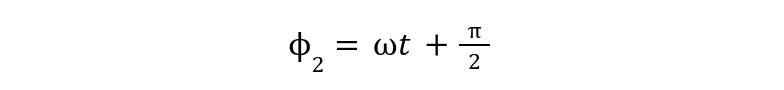
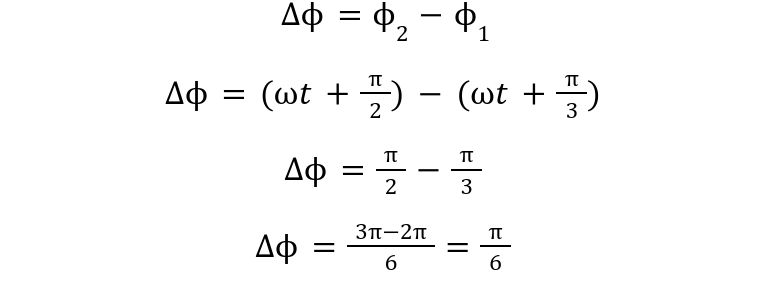
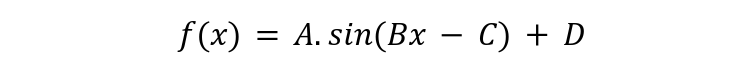
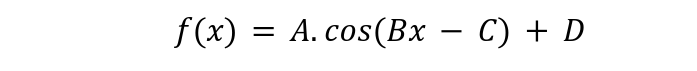
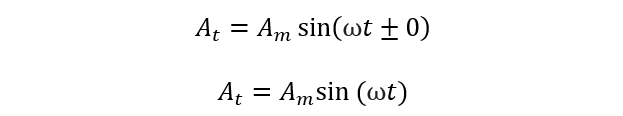
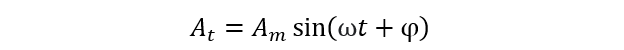
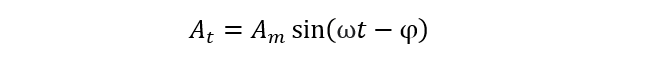
 Example: Calculating the Phase Shift
Example: Calculating the Phase Shift