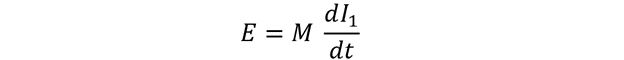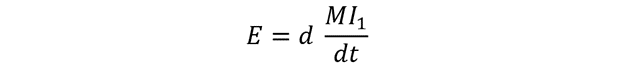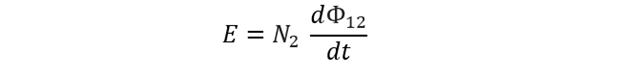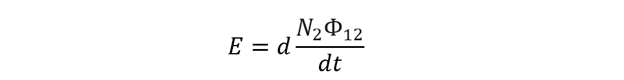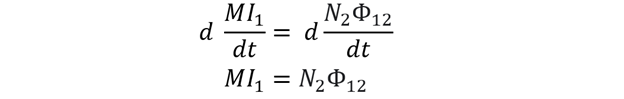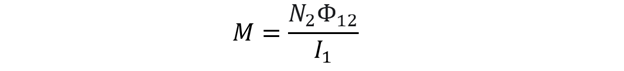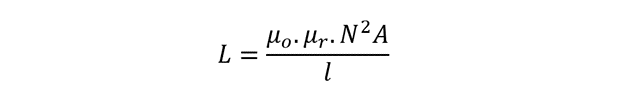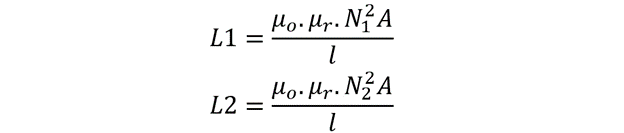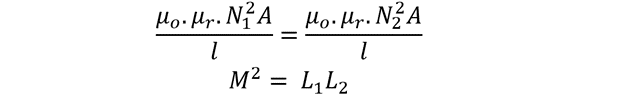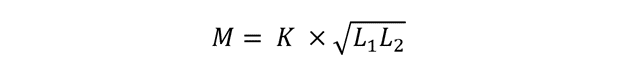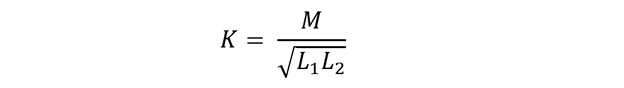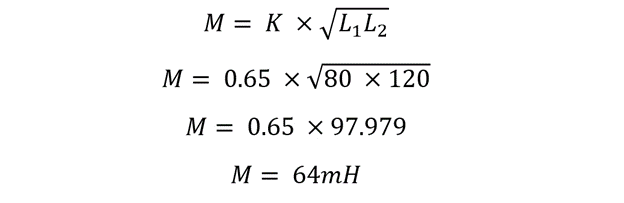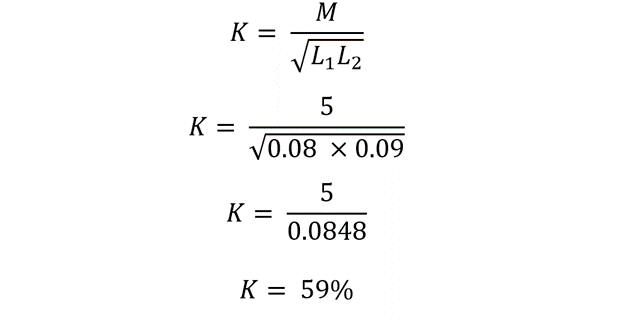Mutual Induction
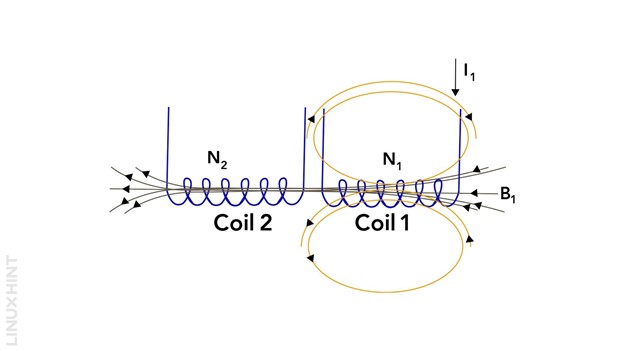
A current-carrying coil produces a magnetic field around it. When two current-carrying coils are brought close to each other, the magnetic fields of the two coils interact with each other resulting in a phenomenon known as mutual induction. As a result of this interaction, an emf is induced in another coil.
Derivation of Formula for Mutual Induction
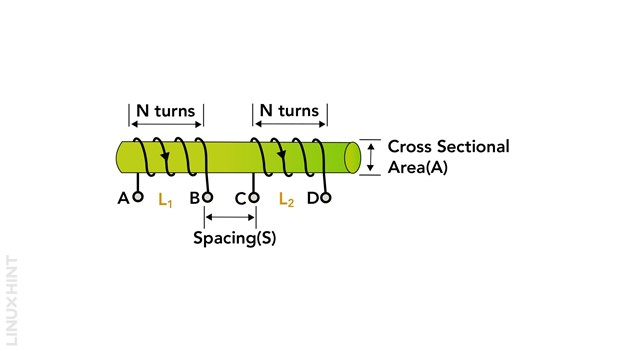
Consider two current-carrying coils wound on a common iron core base as shown below:
As per the definition of mutual inductance, mutual inductance occurs when the time rate of change of current in a coil gives rise to emf in another:
Rearranging the above equation:
Faraday’s law states that induced voltage varies directly with changing magnetic flux. This is expressed as:
Rearranging the above equation:
Equating the above two equations gives:
Mutual inductance can be derived now as:
We can derive another expression for mutual inductance from the self-inductance situation as well. In self-inductance, induced emf is developed in the same coil due to its changing magnetic field.
The self-inductance for an electromagnet is provided as:
The above expression in case of two windings shall be:
By equating the above equations:
Mutual inductance can be derived now as:
However, it is an idealistic case where the two coils shall have 100% magnetic flux coupling in between them.
Coupling Coefficient
In practical cases, a fraction of the above-assumed 100% magnetic flux will interact between coils. This fraction is known through a coefficient ‘K’ called the coupling coefficient.
A more practical version of the above equation shall be:
The coupling coefficient is expressed as:
Example – Calculating Mutual Inductance
Consider an inductor of 80mH placed on a common iron core with another inductor of 120mH. They have been positioned in a manner that almost 65% of the magnetic flux from the first coil is passing through the flux of the next coil. What will be mutual inductance between them?
In the above situation, the magnitude of two inductors along with the percentage of magnetic flux coupling is known. The above-derived expression of mutual inductance can be used as:
Example – Calculating Coupling Coefficient
Two coils with inductances of 80mH & 90mH were wound on an iron core, while the mutual inductance between them is 5H. What would be the probable coupling percentage of magnetic fluxes between them?
Using the above-derived relation for mutual induction, the coupling coefficient is given by:
Conclusion
Mutual induction is responsible for the operation of many electrical machines. These include transformers, generators, metal detectors, and wireless mobile phone charges. In all of these devices, the changing magnetic flux is responsible for the induction of current.