What is the RMS Value of Voltage or Current?
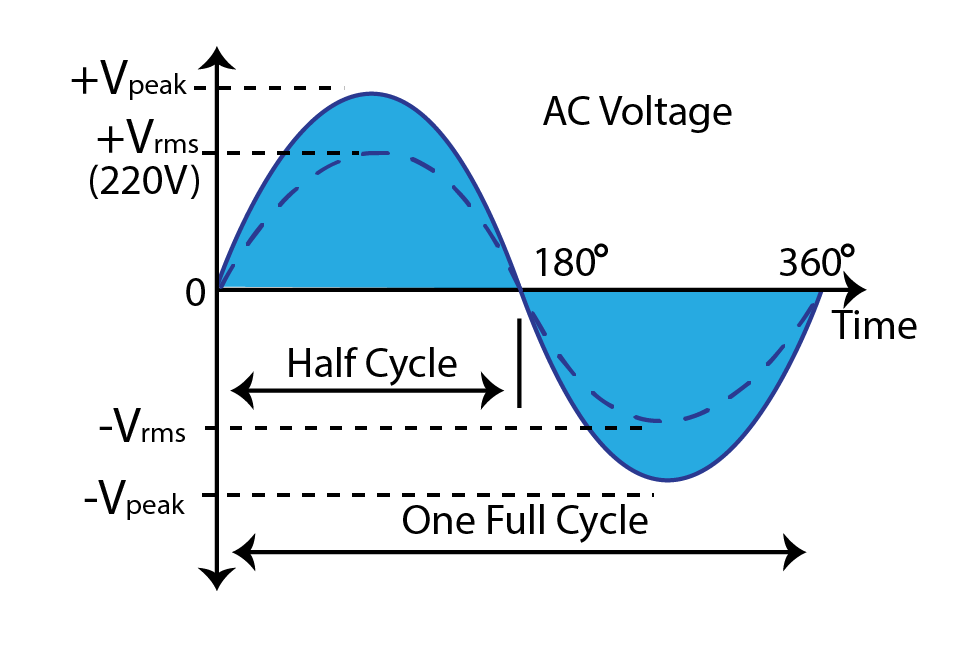
The RMS value of voltage or current is the effective value of AC voltage or current that has an effect similar to a DC source. The symbols that represent RMS value are VRMS or IRMS. They are calculated using instantaneous values of voltage or current from sinusoidal. This is because AC voltage and current change with every instant of time. Therefore, the RMS value tells the ability of AC voltage or current that it can produce power equivalent to its DC value.
For instance, the main supply for domestic use in Pakistan is 220V AC. So, this cannot be the value of sinusoidal AC waveform, instead, it is the RMS value or DC equivalent of AC which means that the AC voltage supplied to homes has the same power-delivering capacity as that of 240V DC. RMS Voltage Equivalent is shown below
Methods for Calculation of RMS Value of AC Voltage or Current
There are mainly two methods that are used for the calculation of RMS value.
1. Graphical Method
It is done by dividing the area under the sinusoidal into patches and then taking the square root of average squares of individual values.
RMS Voltage by Graphical Method
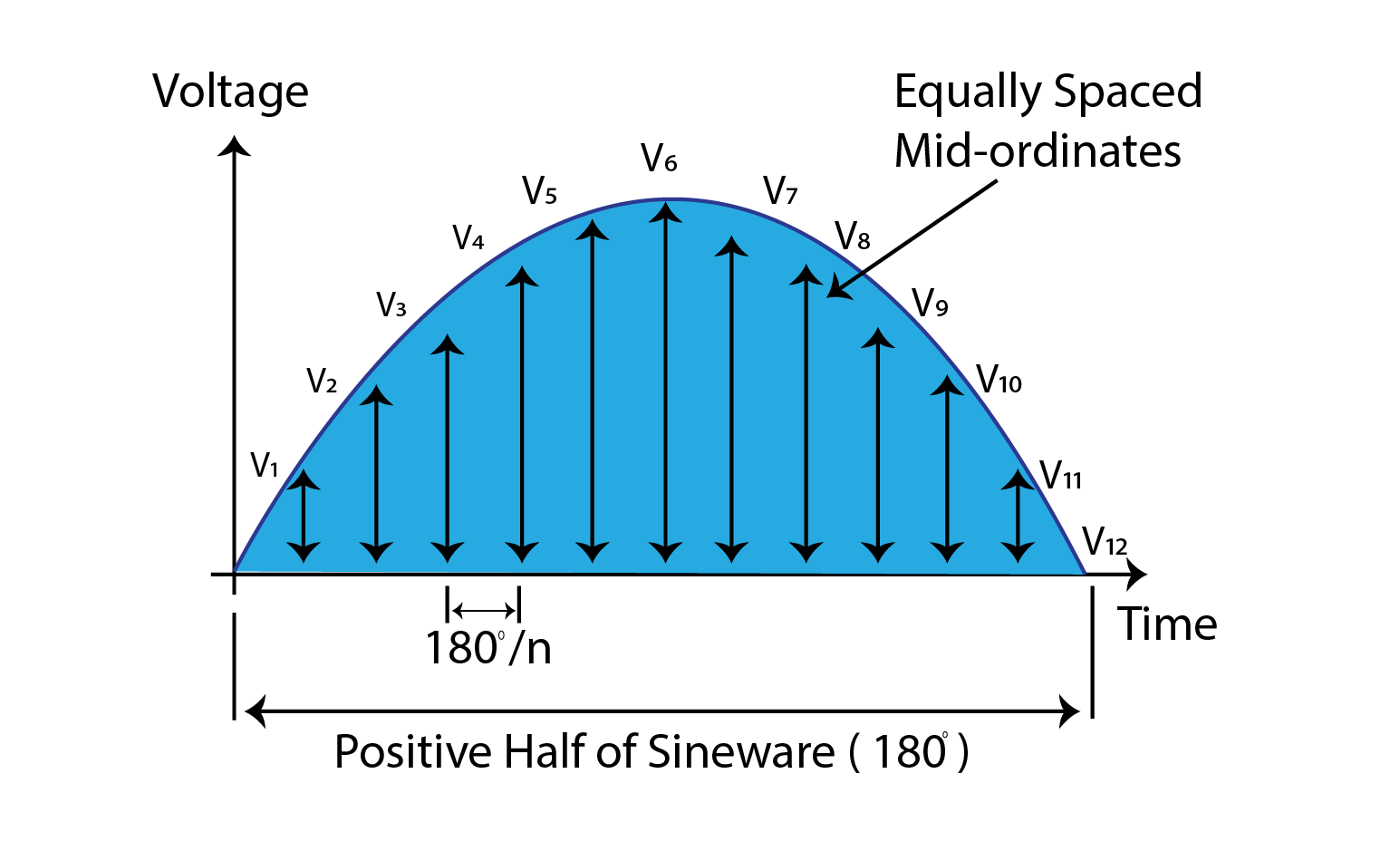
This method can be performed on both positive and negative half cycles. So, for convenience, we can take a positive half-cycle. We will divide the half cycle into small patches by taking values of voltage with equal differences. There can be a ‘n’ number of patches.
So, let us suppose that the peak value of voltage is 30V, and we suppose 10 mid-values for voltages at equal differences along the positive half cycle.
| Voltage | 16.2V | 22.8V | 26.2V | 29.0V | 30.0V | 29.0V | 26.2V | 22.8V | 16.2V | 0V |
| Angle | 18° | 36° | 54° | 72° | 90° | 108° | 126° | 144° | 162° | 180° |
In the above table, it can be seen that voltage values are taken at n° that are equally spaced. Now, the formula to calculate the RMS value for voltage is:
Putting values in the equation
So, through the graphical method, the DC equivalent or RMS value of the AC sinusoidal waveform is 23.5V.
2. Analytical Method
It is done by using trigonometric expressions and generalizing the expression for RMS value.
RMS Voltage Analytical Method
The graphical method is accurate, but it is not feasible for long sinusoidal waves because of extensive calculations. So, the analytical method is used to make the task easier.
Integration technique is used in an analytical method to calculate RMS Value. For any time, instant t, the value of voltage for time T is given by:
Now to calculate the RMS Value of voltage, this instantaneous value is integrated over a time T and then its square root is taken which comes out to be as shown below:
By integrating it from 0° to 360°:
Putting values of limits in this equation gives the RMS Voltage Equation:
So, from the above formula, we can say that the RMS value of voltage can be calculated by multiplying the peak value of voltage with a factor of 0.707.
If we apply this formula to the example explained above in the graphical method, where Vm is 30V, we will get:
This is the same value as that of the value calculated from the graphical method. Therefore, the RMS value can be calculated by using the above-generalized formula. A similar formula will be used for current to calculate the RMS value of current.
Some other expressions for calculating RMS value that is derived from the generalized formula are given:
 Conclusion
Conclusion
We have learned that the RMS value is very useful for representing the magnitude of AC sinusoidal. However, through graphical methods, its calculations are so extensive that they cannot be adopted for long sinusoidal. So, we have derived a general formula that gives the RMS value through peak voltage, peak-to-peak voltage, or average value of voltage. The important point here is that RMS Value is not the average value, instead it is the average of squared values of voltages. The value of AC shown on the multimeter is also an RMS value. This RMS value is required to rate equipment.

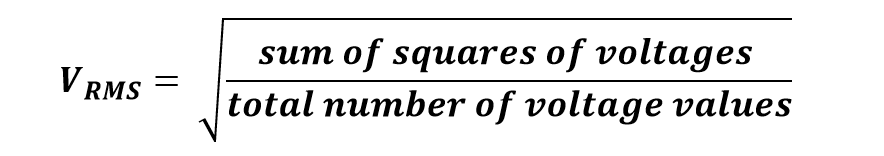
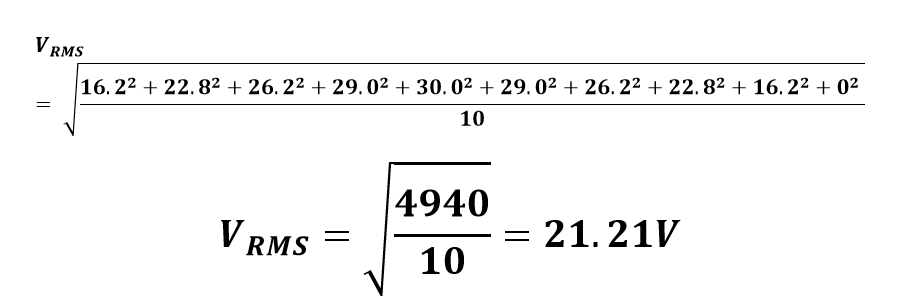
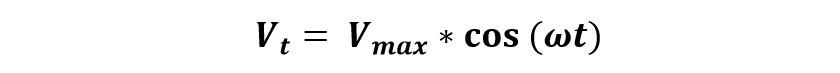
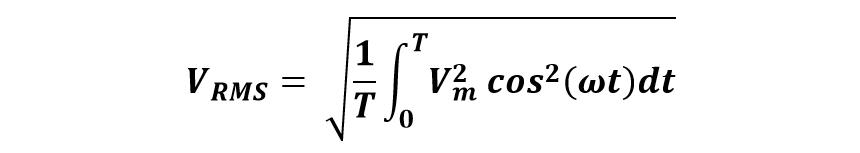
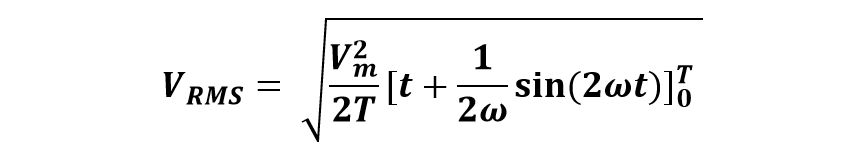
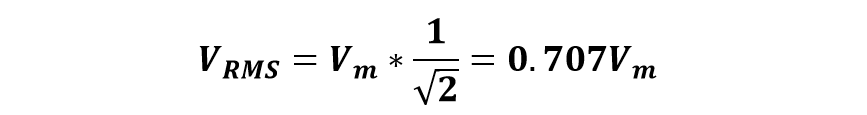
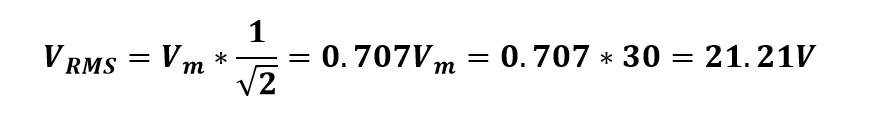
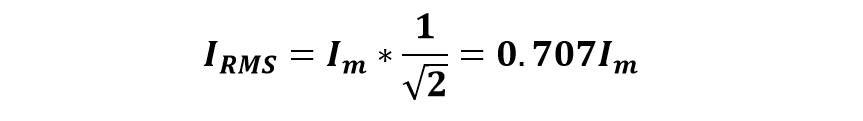
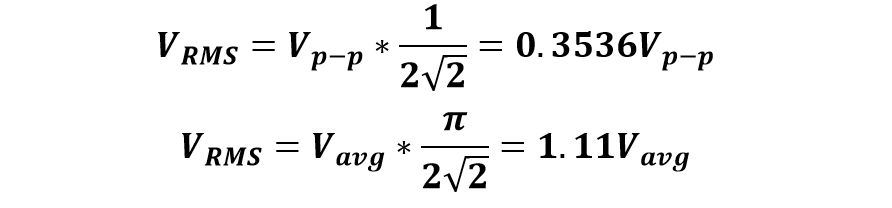 Conclusion
Conclusion