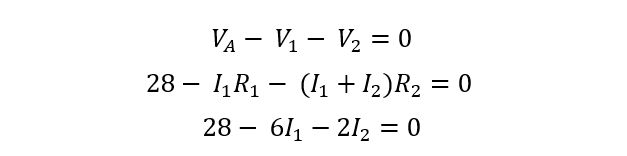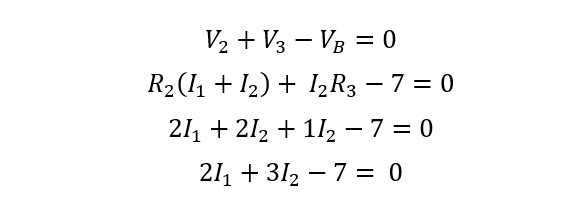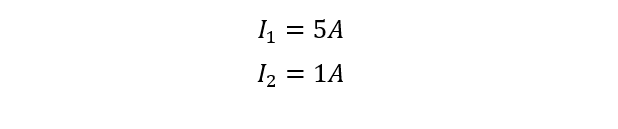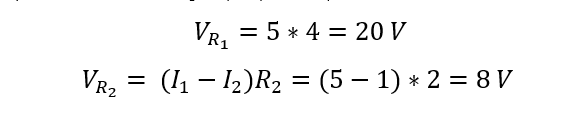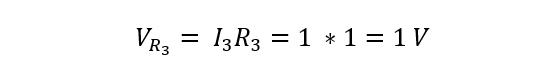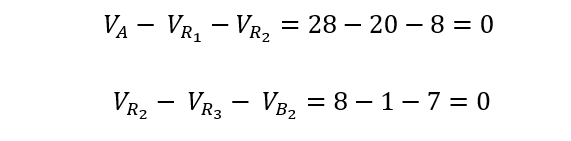A Guide to Mesh Current Analysis

In electrical circuit analysis, mesh current analysis is a powerful method used to determine the current flowing through various components within a circuit. By dividing the circuit into interconnected loops and assigning mesh currents, engineers and technicians can efficiently analyze and predict the behavior of complex electrical networks. In this article, we will explore the concept of mesh current analysis, outline its procedure, and provide an example to illustrate its application.

What is Mesh Current Analysis?

Mesh current analysis, also known as the mesh-current method or loop analysis, is a systematic approach used to solve electrical circuits by focusing on the fundamental principle that the sum of voltages around any closed loop in a circuit is equal to zero. By assigning mesh currents as variables, mesh current analysis simplifies complex circuit equations and enables efficient analysis of electrical networks.

Procedure for Mesh Current Analysis

1. Identify Essential Meshes: Begin by identifying the essential meshes or loops within the circuit. These meshes typically include closed paths that cover all the circuit elements, such as resistors, capacitors, or voltage sources.

2. Assign Mesh Currents: Assign a mesh current to each essential loop. Typically, clockwise currents are chosen as positive, but the actual direction doesn’t affect the final results as long as consistency is maintained throughout the analysis.

3. Apply Kirchhoff’s Voltage Law (KVL): For each mesh, apply Kirchhoff’s Voltage Law, which states that the sum of voltage drops around any closed loop is equal to zero. Express the equations in terms of the mesh currents and the circuit elements present in each loop.

4. Solve Simultaneous Equations: With the KVL equations established, solve the simultaneous equations to determine the mesh currents. This can be accomplished through various mathematical techniques, such as matrix methods or nodal analysis.

5. Calculate Desired Values: Once the mesh currents are known, calculate any desired values within the circuit, such as voltage drops across specific components or power dissipation across resistors.

Example: Mesh Current Analysis

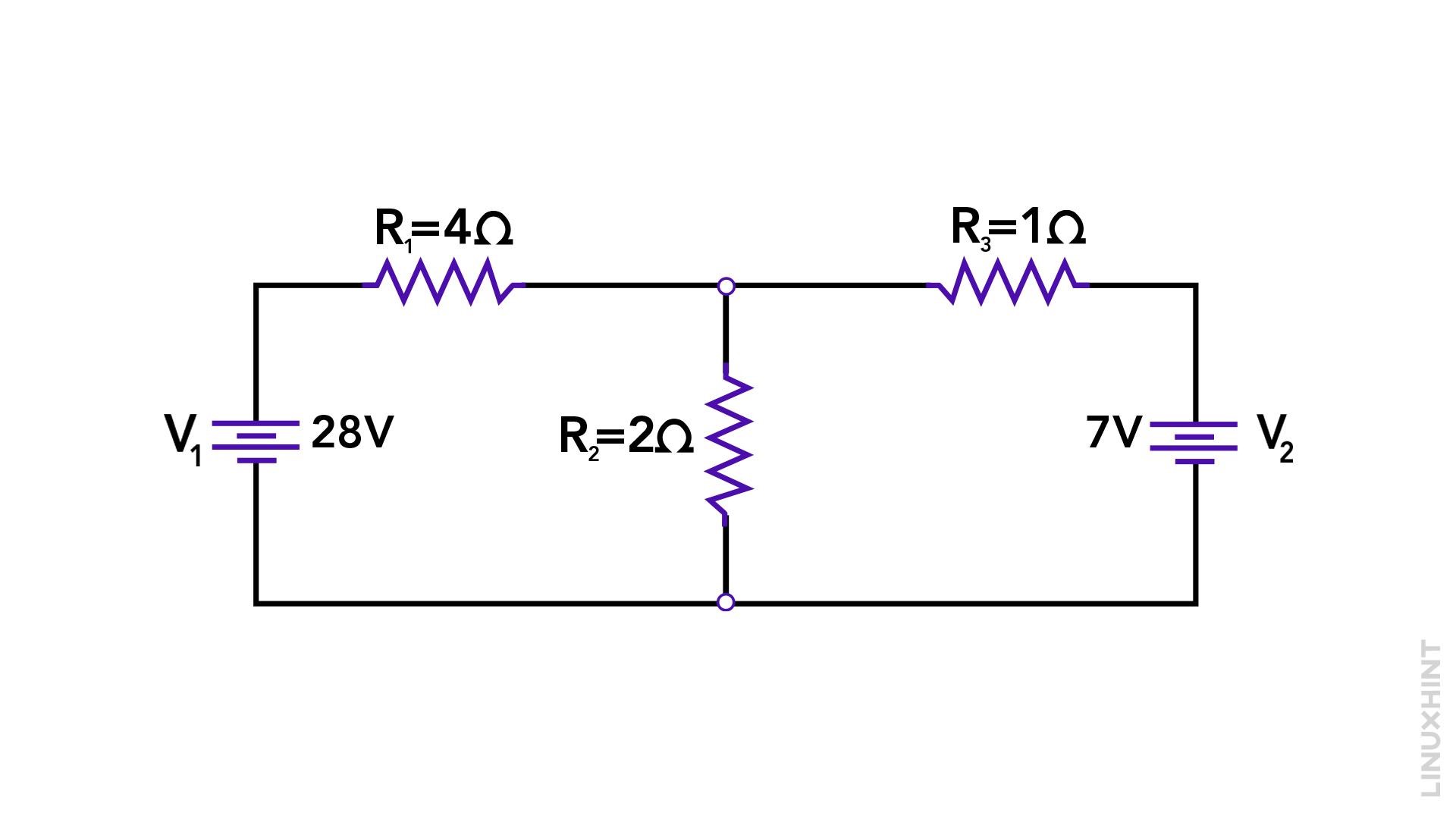
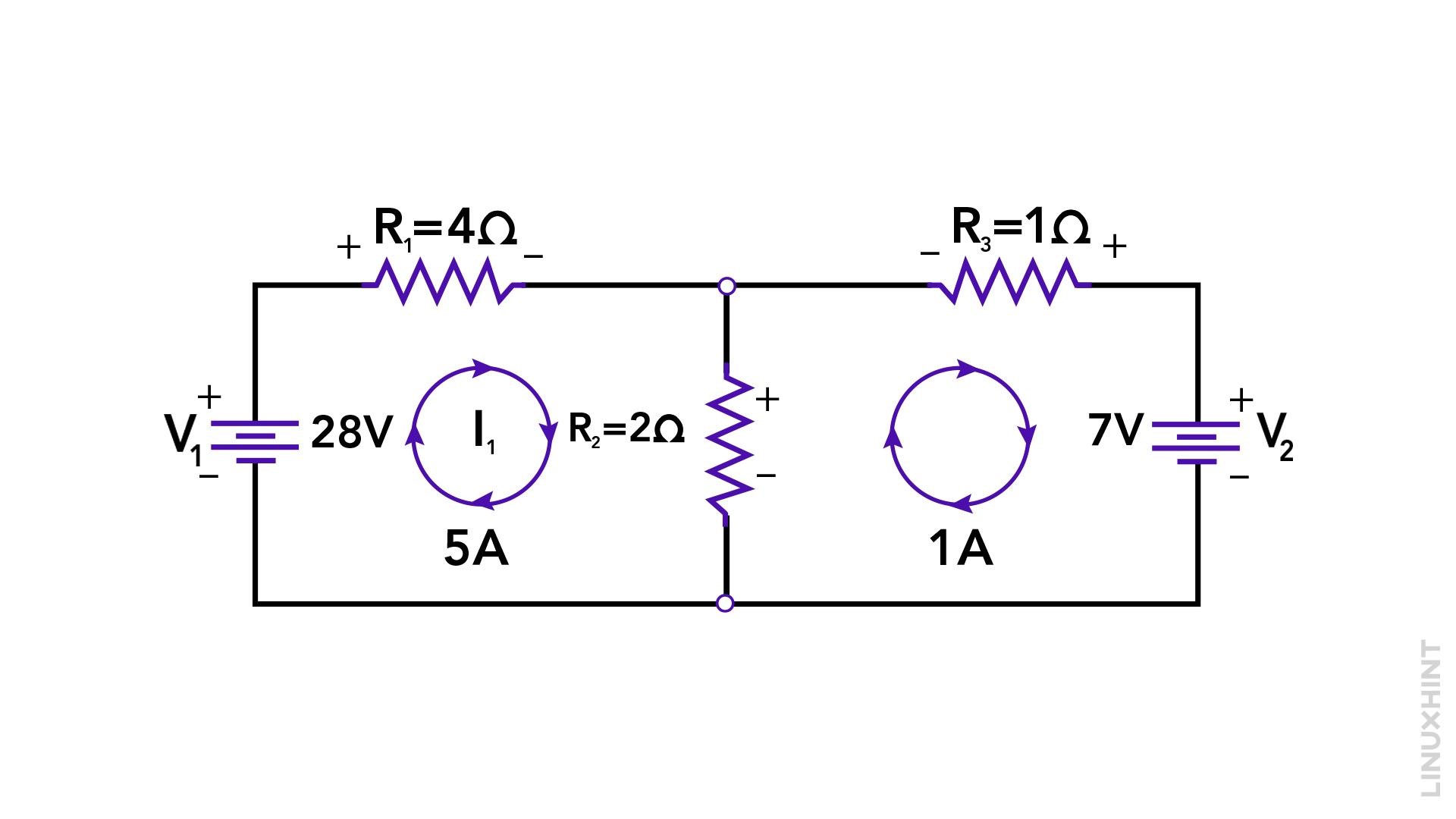
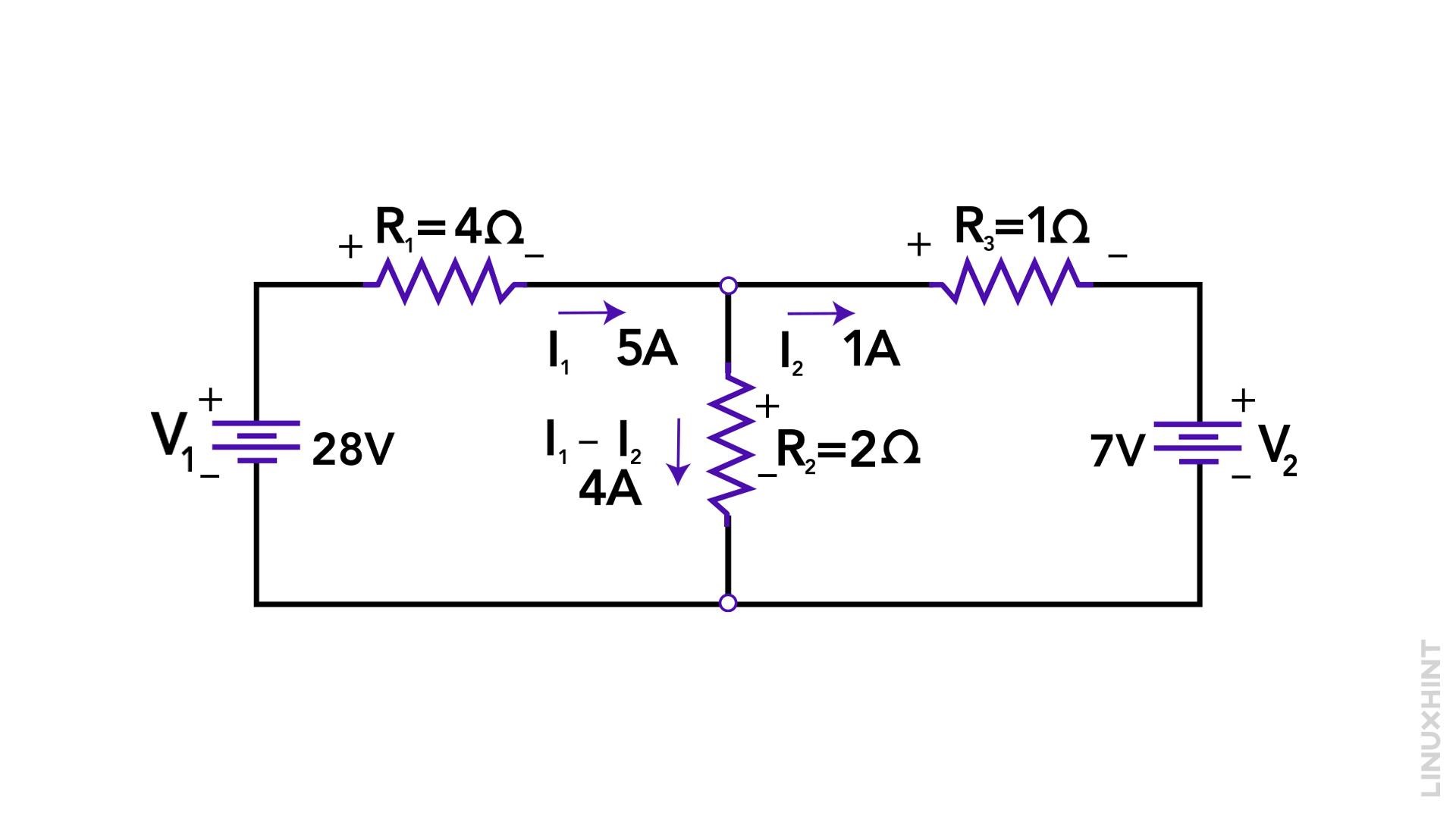
Assume the resistances are R₁ = 4 ohms, R₂ = 2 ohms, R₃ = 1 ohms. There are two voltage sources, V₁ having a voltage of 28 volts and V₂ having a voltage of 7 volts.

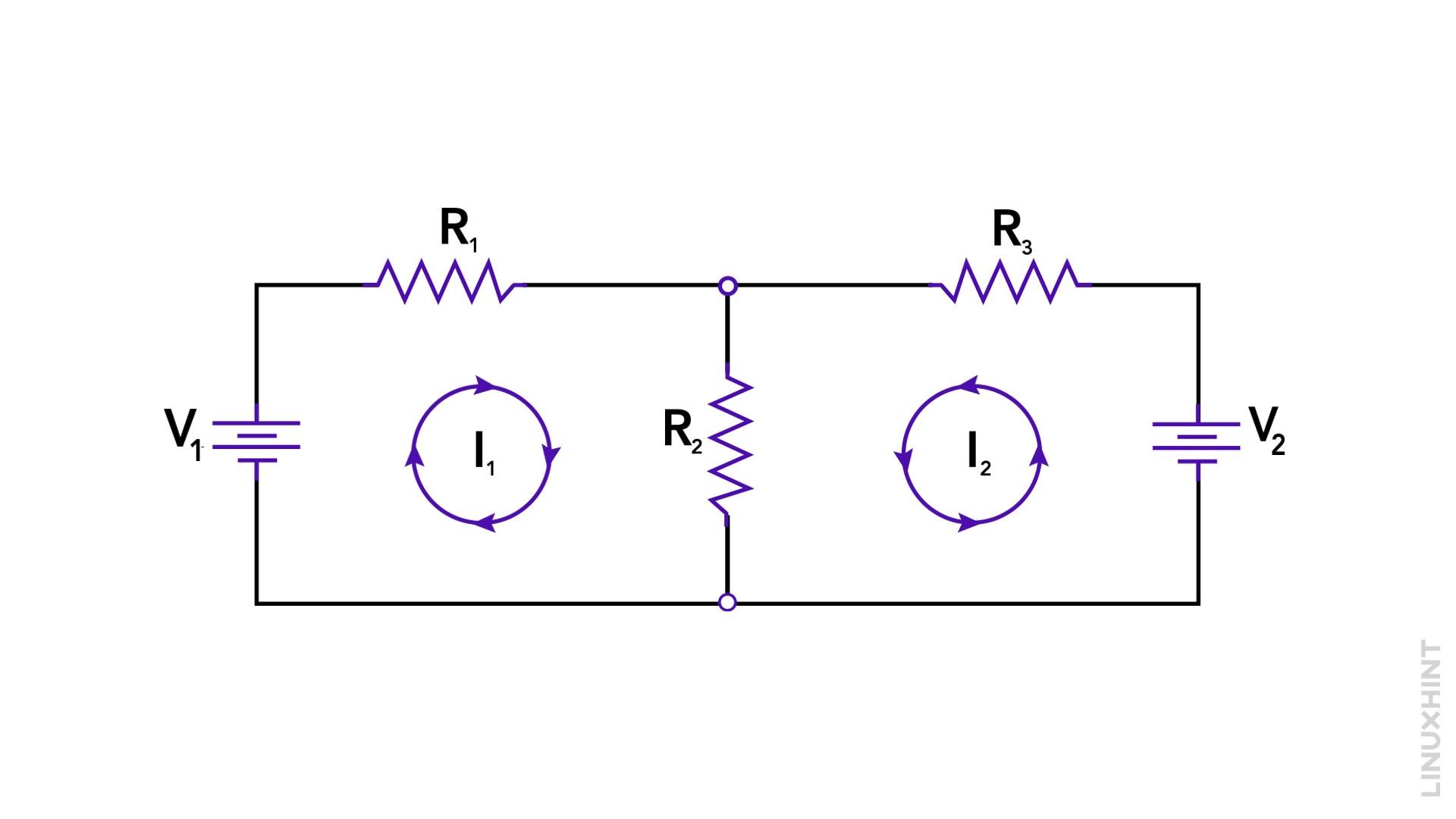
1. Identify Essential Meshes: In this circuit, there are two essential meshes: Mesh 1 (formed by R₁ and R₂) and Mesh 2 (formed by R₂, and R₃):

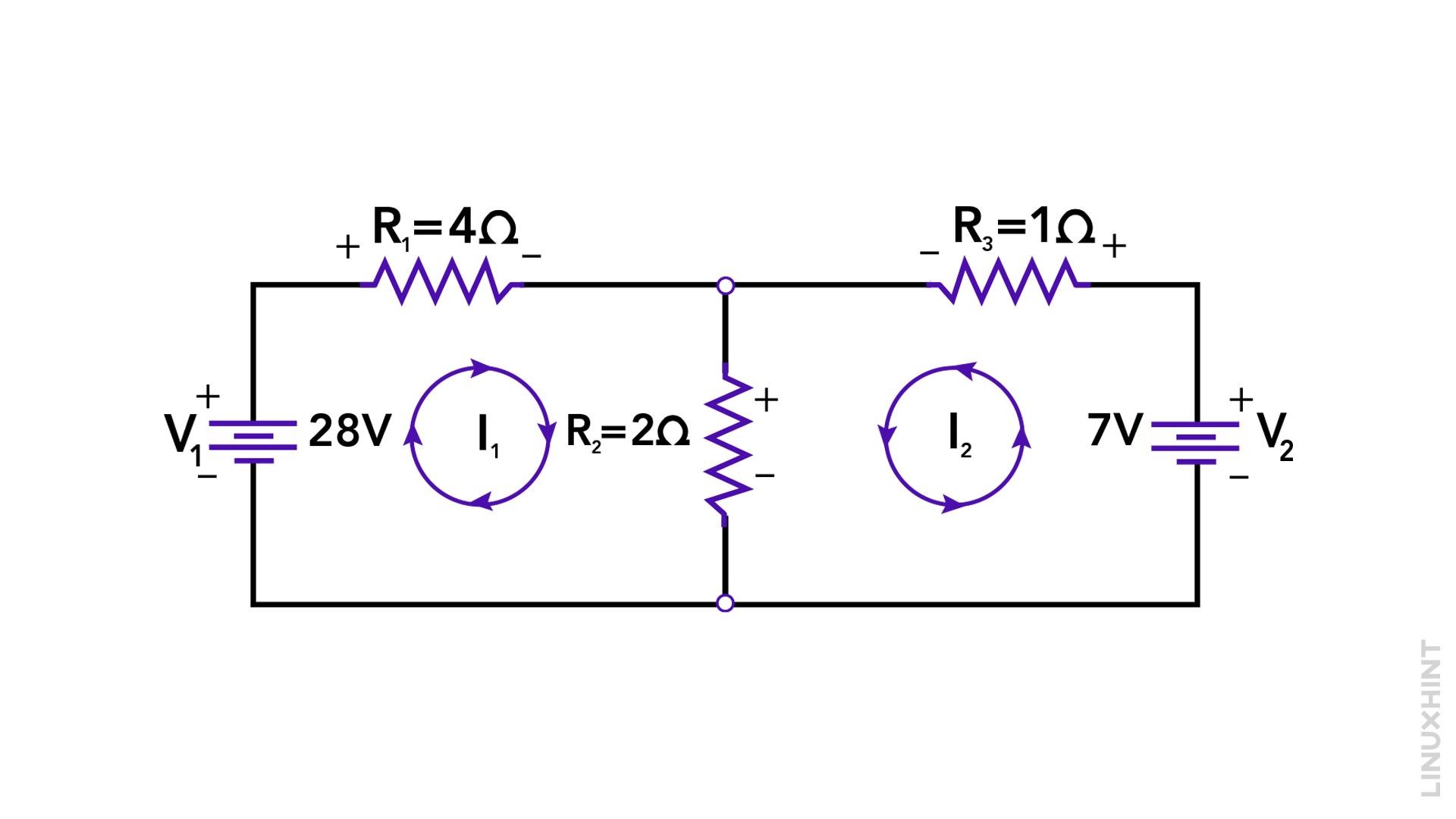
2. Assign Mesh Currents: Assign clockwise mesh currents (I₁ and I₂) to Mesh 1 and Mesh 2, respectively.

3. Apply KVL: Applying KVL to Mesh 1 and Mesh 2, we get:

This is the first equation and since it has two unknowns that is I₁ and I₂ so to find them it is necessary to have two equations so for the mesh the equation will be:

4. Solve Simultaneous Equations: Rearrange the equations to solve for I₁ and I₂ and after solving the values of I₁ and I₂ are:

5. Calculate Desired Values: In this example, if Vs = 28 volts and the resistances are as mentioned earlier, solving the equations will yield the values of I₁ and I₂, which can then be used to calculate any desired values such as voltage drops or power dissipation.

Now to verify Kirchhoff’s law and the values we calculated for the voltage drop across the resistors:

Conclusion

Mesh current analysis is a valuable technique for analyzing electrical circuits. By applying Kirchhoff’s Voltage Law and assigning mesh currents as variables, engineers can simplify complex circuit equations and efficiently solve for current flow, voltage drops, and power dissipation.