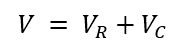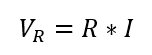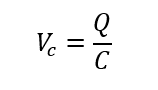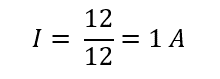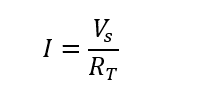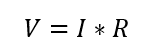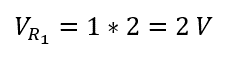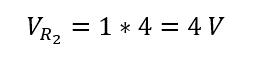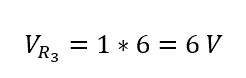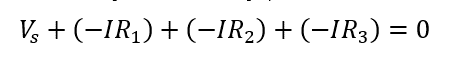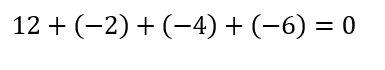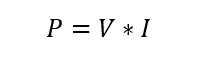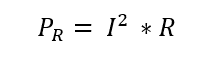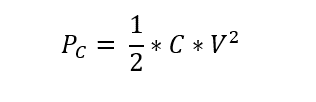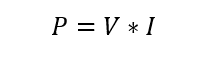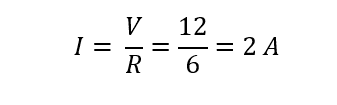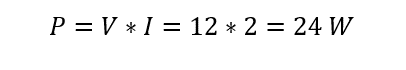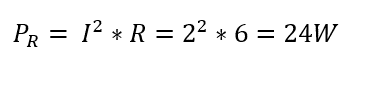In circuit analysis, two fundamental principles play a crucial role: Kirchhoff’s Voltage Law (KVL) and the Conservation of Energy. These principles enable us to understand and analyze the behavior of electrical circuits and ensure the efficient utilization of energy. In this article, we will delve into the concepts of Kirchhoff’s Voltage Law and the Conservation of Energy, providing a clear understanding of their importance and the equations associated with them.
What is Kirchhoff’s Voltage Law (KVL)
This law claims that each closed loop in an electrical circuit has zero voltage as the sum of all surrounding voltages. To put it another way, in a closed loop circuit, the algebraic total of the voltage rises and falls is always equal to zero.
Explanation of Kirchhoff’s Voltage Law (KVL)
Kirchhoff’s Voltage Law can be understood by considering an electrical circuit with various components such as resistors, capacitors, and inductors. For the sake of explanation, I have thought about a straightforward circuit made up of a series connection between a voltage source (V), a resistor (R), and a capacitor (C).
According to KVL, the sum of voltage drops across each component in a closed loop should be equal to the applied voltage. Mathematically, it can be represented as:
Where:
V represents the applied voltage from the source.
VR represents the voltage drop across the resistor.
VC represents the voltage drop across the capacitor.
Ohm’s Law, which states that the voltage drop across a resistor is equal to the product of its resistance (R) and the current (I) flowing through it, can be used to calculate the voltage drop across a resistor. Mathematically, it can be represented as:
Similarly, the voltage drop across a capacitor can be determined by the equation:
Where:
Q represents the charge stored in the capacitor.
C denotes the capacitance of the capacitor.
Example for Kirchhoff voltage Law
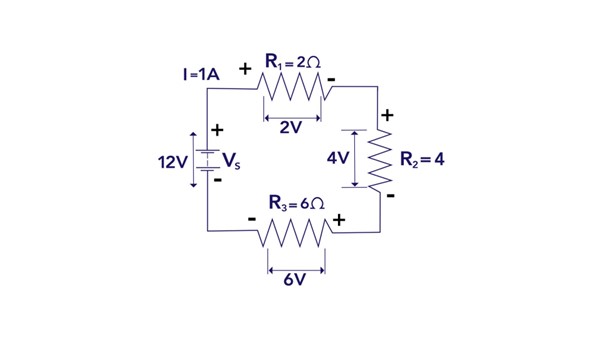
Here is a simple circuit with three resistors (R1, R2, R3) connected in series. This example will demonstrate how Kirchhoff’s Voltage Law (KVL) holds true by showing that the sum of all voltages in the loop is equal to zero.
In a series circuit, the total resistance is the sum of individual resistances:
Suppose some arbitrary resistance values for each resistor:
Resistor 1 (R1) = 2 ohms
Resistor 2 (R2) = 4 ohms
Resistor 3 (R3) = 6 ohms
Now the equivalent resistance will become 12, next to verify KVL, we need to calculate the voltage drops across each resistor, and before that, we need to calculate the current in the circuit and for that, the following equation can be used:
Now if we place the value of source voltage that is 12 volts and the equivalent resistance that is 12 ohms then the above-given equation will be:
So now the current value is 1 A, and since it is a series circuit, the current will be the same across each resistor. However, the voltage across the resistor will be different, so now we will calculate it across each resistor by using the following equation:
Now the voltage drop across the resistor R1 will be:
The voltage drop across the resistor R2 will be:
The voltage drop across the resistor R3 will be:
Now to verify the Kirchhoff voltage law, use the following equation:
Now place the values of the current and voltage in the equation given above:
According to KVL, the sum of the voltage drops around a closed loop is equal to zero, and the result above proves the Kirchhoff Law.
What is the Conservation of Energy
It is a fundamental law of physics that energy cannot be generated or destroyed; rather, it can only be changed from one form to another, and this law is called the conservation of energy. This law is equally applicable to electrical circuits, where the energy provided to a circuit is either consumed by the components or converted into another form.
Explaining Conservation of Energy
The Conservation of Energy principle is applied in electrical circuits to ensure that the energy supplied to the circuit is preserved and appropriately utilized. In any electrical circuit, the total power supplied must equal the sum of power consumed and dissipated.
The power supplied by a voltage source can be calculated using the equation:
Where:
P represents the power supplied.
V is the voltage supplied by the sources connected.
I am the current that flows in the circuit.
The power consumed by a resistor can be calculated using the equation:
The power dissipated by a capacitor can be calculated using the equation:
Example for conservation of energy
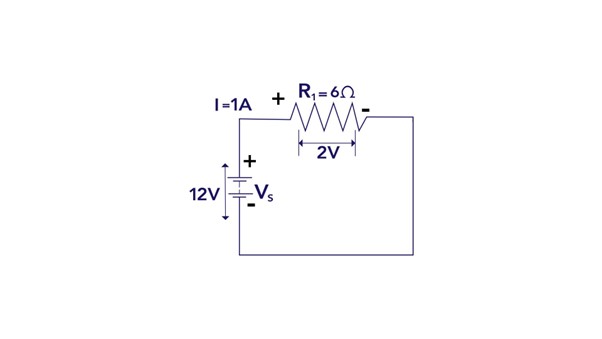
Suppose a circuit consisting of a battery (V) is connected to a resistor (R) and the battery provides a constant voltage, and the resistor converts electrical energy into heat energy.
Here, for the sake of demonstration, I have taken the voltage equal to 12 and the value of resistance is equal to 6 ohms. The total power supplied by the battery must match the total power used by the resistor by the conservation of energy concept.
To calculate the power supplied by the battery, we can use the formula:
Where P represents power and I denote the current flowing through the circuit.
To calculate the power supplied by the source current in the circuit should be known and for that use Ohm’s Law:
Now, let’s calculate the power supplied by the battery:
The power used by the resistor should be equal to the power supplied by the battery, based on the principle of energy conservation. The following formula can be used to determine the power used by the resistor in this situation:
Where PR represents the power consumed by the resistor.
As we can see, the power supplied by the battery (24 watts) is equal to the power consumed by the resistor (24 watts). This example demonstrates the principle of the Conservation of Energy, where the energy supplied to the circuit is converted into another form (heat in this case) without any loss or gain in the overall energy.
Conclusion
Kirchhoff’s Voltage Law and the Conservation of Energy are vital concepts in circuit analysis, helping engineers and scientists understand and analyze electrical circuits. Kirchhoff’s Voltage Law states that the in a closed loop circuit sum of voltages is zero, providing an effective way for circuit analysis. On the other hand, the Conservation of Energy principle ensures that energy is preserved and effectively utilized within an electrical circuit by applying these principles and the associated equations.