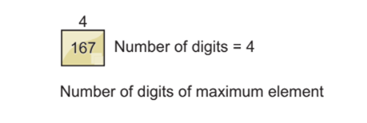A radix or base is a representation of a number that shows how many digits are required to represent a positional number. For example, to represent the binary number, the radix value is 2 (we represent the binary either with 0 or 1). To represent the decimal number, the radix value is 10 (we represent the decimal number with numbers 0 to 9).
How the Redix Sort Algorithm Works
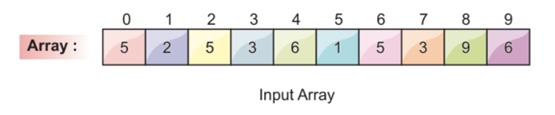
Let’s assume we have the following array list and we want to sort this array using the radix sort:
We use two more concepts in this algorithm, which are:
-
- Least significant digit
- Most significant digit
1. Least significant digit (LSD): The exponent value of a decimal number that is extremely close to the rightmost position is referred to as the LSD.
For example, the decimal number “2563” has the least significant digit value of “3”.
2. Most significant digit (MSD): The MSD is the LSD’s exact inverse. An MSD value is the non-zero leftmost digit of any decimal number.
For example, the decimal number “2563” has the most significant digit value of “2”.
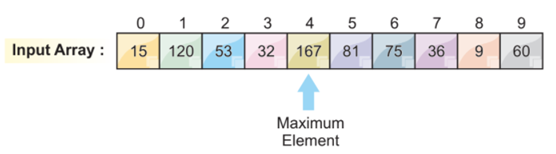
Step 1: Look for the Most Important Element (Maximum Value)
As we already know, this algorithm works on the digits to sort the numbers. So, for that, this algorithm requires the maximum number of digits for the iteration. Our first step is to find out the maximum number of elements in this array. After finding the maximum value of an array, we have to count the number of digits in that number for the iterations.
Step 2: Count the Number of Digits of the Maximum Element
We have to count the number of digits of the maximum element of an array because then we can find out how many iterations we require to sort the array.
So, as we already found out, the maximum element is 167 and the number of digits is 3. We need three iterations to sort the array.
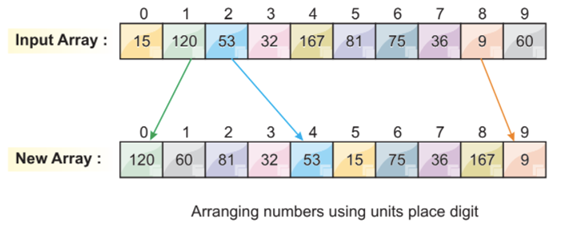
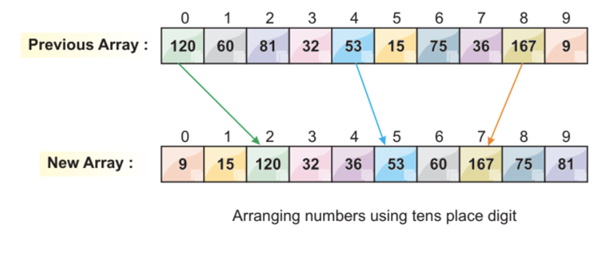
Step 3: Sorting the Elements by Least Significant Digit
The first digit arrangement is done by the least significant digit. From the following image, we can see that all the smallest, least significant digits are arranged on the left side. In this case, we focus on the least significant digit only.
One more thing we can notice here is that some digits are automatically sorted, even if their unit digits are different, but the others are the same.
For example, the numbers 36 at index position 7 and the number 32 at index position 3 both have different unit digits but have the same other number, which is 3. Obviously, number 32 comes before number 36. After the first element arrangements, we can see that now, 32 comes before 36 which is automatically sorted.
Step 4: Sorting the Elements According to the Next Digit (Tens Digit)
Now, we arrange the elements of the array through the tenth place digit. As we already know, this sorting has to be finished in 3 iterations because the maximum number of elements has 3 digits. This is our second iteration and we can assume that most of the array elements are sorted after this iteration.
The given results show that most of the array elements are already sorted (below 100). If we had only two digits as our maximum number, only two iterations are enough to get the sorted array.
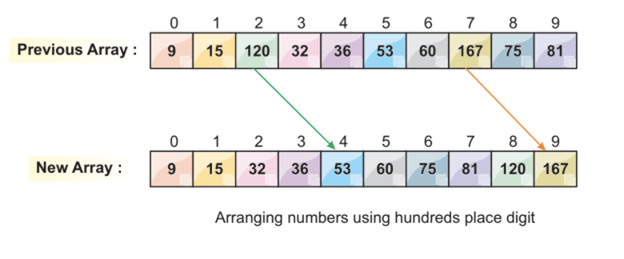
Step 5: Sorting the Elements Based on the Most Significant Digit
Now, we enter the third iteration based on the most significant digit (hundreds place). This iteration sorts the three digit elements of the array. After this iteration, all elements of the array are in sorted order.
After arranging the elements based on the MSD, our array is now fully sorted.
We understood the concepts of the Radix Sort Algorithm. But we need one more algorithm to implement the Radix Sort, and that is the Counting Sort Algorithm. Let’s understand this counting sort algorithm.
Counting Sort Algorithm
We now explain each step of the counting sort algorithm.
The provided array is our input array, and the numbers that are shown above the array are the index numbers of the corresponding elements.
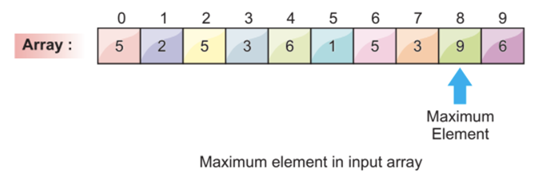
Step 1: Search the Maximum Element
The first step in the counting sort algorithm is to search for the maximum element in the whole array. The best way to search for the maximum element is to traverse the whole array and compare the elements in each iteration – the greater value element is updated until the end of the array.
During the first step, we found that the max element is 9 at index position 8.
Step 2: Make a New Array of Comparable Sizes
We create a new array of similar sizes. As we already know, the maximum value of the array is 9, so there will be a total of 10 elements. As a result, we require a maximum array size of + 1.
As we can see in the previous image, we have a total array size of 10 with values of 0. In the next step, we fill this count array with sorted elements.
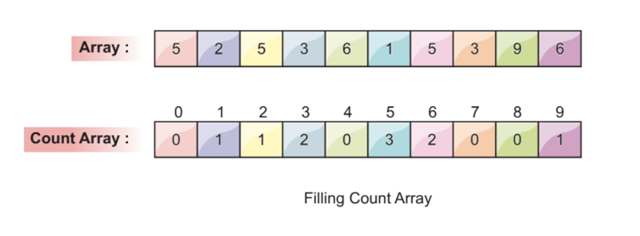
Step 3: Fill the New Array According to the Frequency of Each Element
In this step, we count each element and, according to their frequency, fill in the corresponding values in the array.
For example, as we can see, element 6 is present two times in the input array. So, we enter the frequency value of 2 at index 6.
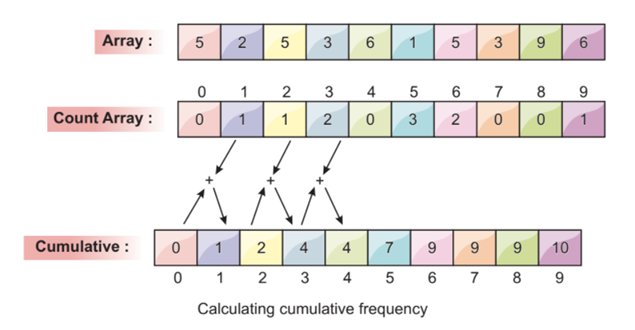
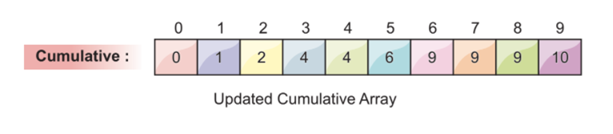
Step 4: Determine the Cumulative Frequency
Now, we count the cumulative frequency of the filled array. This cumulative frequency is used later to sort the input array.
We can calculate the cumulative frequency by adding the current value to the previous index value, as shown in the following screenshot:
The last value of the array in the cumulative array must be the total number of elements.
Step 5: Sorting the Array by Commutative Frequency
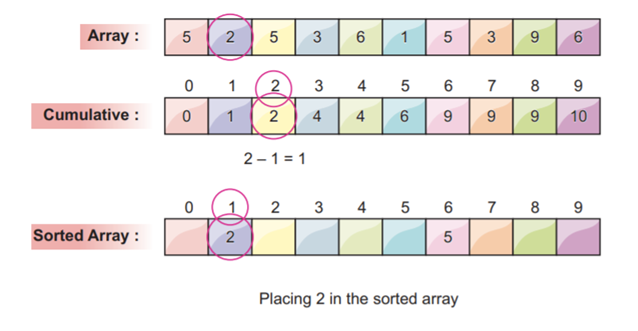
Now, we use the cumulative frequency array to map each array element to produce a sorted array.
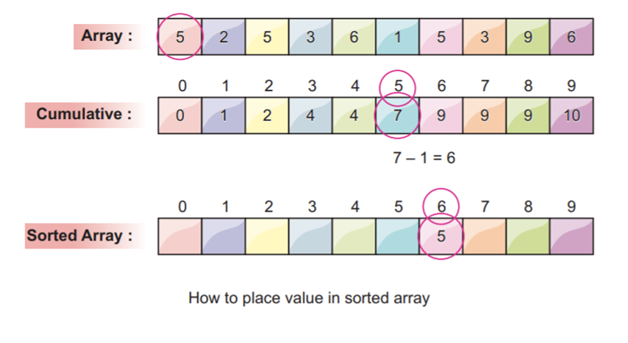
For example, the first element in the array 5 that we choose. Then, the corresponding cumulative frequency value at index 5 which has a value of 7. We decrement the value by 1 and got 6. We place the value 5 in the index at the 6 position and also decrement the cumulative frequency at index 5 by 1.
The cumulative frequency is at index 5 after being decremented by one.
Let’s understand this concept with one more example.
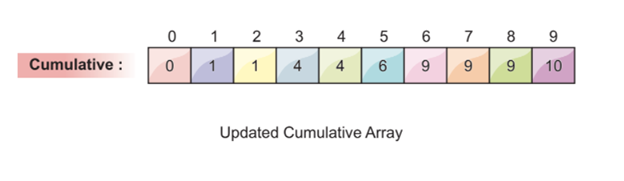
The next element in the array is 2. We choose the index value of 2 in the commutative frequency array. We decrement the value at index 2 and get 1. We place the array element 2 at index position 1. At the end, we decrement the frequency value at index 2 by 1, as shown in the following screenshot:
From the previous sorted array, we can see that only one place is left before 2 (index position 1) and one value less than 2 in the original array, which is 1. So, it goes in the right way of sorting the array.
We do not have to remember to reduce the cumulative value at each iteration. After two of the previous iterations, the cumulative array looks like the following:
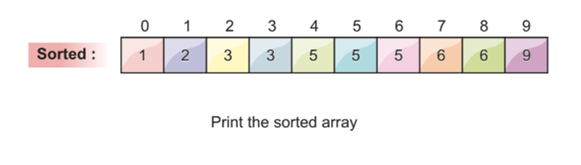
Step 6: Final Array
We run the step 5 until every array elements are filled in the sorted array. After it is filled, our array looks like this:
C++ Program for Radix Sort Algorithm
This example is based on the explanation in this Linux Hint Tutorial
using namespace std;
void radixSortAlgo(int a[], int size_of_a){
// In the first step (step 1), we fina the maximum value in the array.
int maximumNumber = a[0];
for(int i=1;i<size_of_a;i++){
maximumNumber = max(maximumNumber, a[i]);
}
// In the second step (step 2), we are calculating the number of digits of
// the maximum element of the array
int digitsCount = 0;
while(maximumNumber > 0){
digitsCount++;
maximumNumber /= 10;
}
// We are now updating a new array (Steps 3,4 and 5)
for(int i=0;i<digitsCount;i++){
int pwr = pow(10, i);
int new_a[size_of_a];
// This is a count_array which is used for the counting array
// to sort digits 0 to 9.
int count_array[10];
memset(count_array, 0, sizeof(count_array));
// Calculating the frequency of each element of the array
for(int j=0;j<size_of_a;j++){
int num = (a[j]/pwr) % 10;
count_array[num]++;
}
// This is a comulative frequency
for(int j=1;j<10;j++){
count_array[j] += count_array[j-1];
}
// We are mapping the frequency array with each element
// of the array to find out desired position in the updated array
for(int j=size_of_a-1;j>=0;j--){
int num = (a[j]/pwr) % 10;
new_a[count_array[num]-1] = a[j];
count_array[num]--;
}
// Now, we are updating the array with the new array
for(int j=0;j<size_of_a;j++)
a[j] = new_a[j];
}
// Finally,we print the sorted array result
for(int j=0;j<size_of_a;j++)
cout<<a[j]<<" ";
cout<<endl;
}
int main(){
// This array of values will be sorted using the radix sort algorithm.
int a[] = {155, 10, 51, 38, 16, 811, 755, 3, 91, 6};
// We are calculating size of the array
int size_of_a = sizeof(a)/sizeof(size_of_a);
// Calling to Radix Sort Algorithm method
radixSortAlgo(a, size_of_a);
return 1;
}
Output from running C+ Radix Sort
3 6 10 16 38 51 91 155 755 811
linuxhint@DESKTOP:~$
Time Complexity of Radix Sort Algorithm
Let’s calculate the time complexity of the Radix Sort Algorithm.
Step 1: To calculate the maximum number of elements in the entire array, we traverse the entire array. So, the total time required is O(n).
Step 2: Let’s assume that the total digits in the maximum number is k. So, the total time that is taken to calculate the number of digits in a maximum number is O (k).
Steps 3 to 5: These steps work on the digits themselves, so they take O (k) times along with counting the sort algorithm at each iteration – O (k * n).
As a result, the total time complexity is O(k * n).
Conclusion
We studied the radix sort and counting algorithm. There are different kinds of sorting algorithms that are available on the market. The best algorithm also depends upon the requirements. It’s not easy to say which algorithm is best. But on the basis of the time complexity, we are trying to figure out the best algorithm. And on the basis of that, radix sort is also one of the best algorithms for sorting.