How to list disk devices in Linux with lsblk
The proper way to list block devices such as hard disks is using the command lsblk.
Note: the -a flag forces lsblk to list also empty devices.
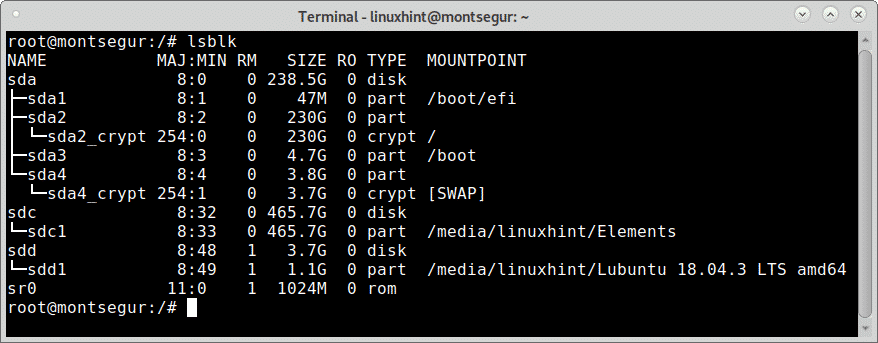
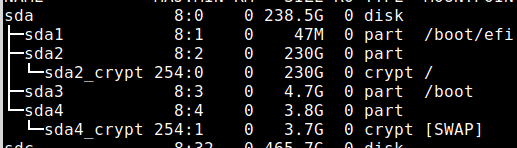
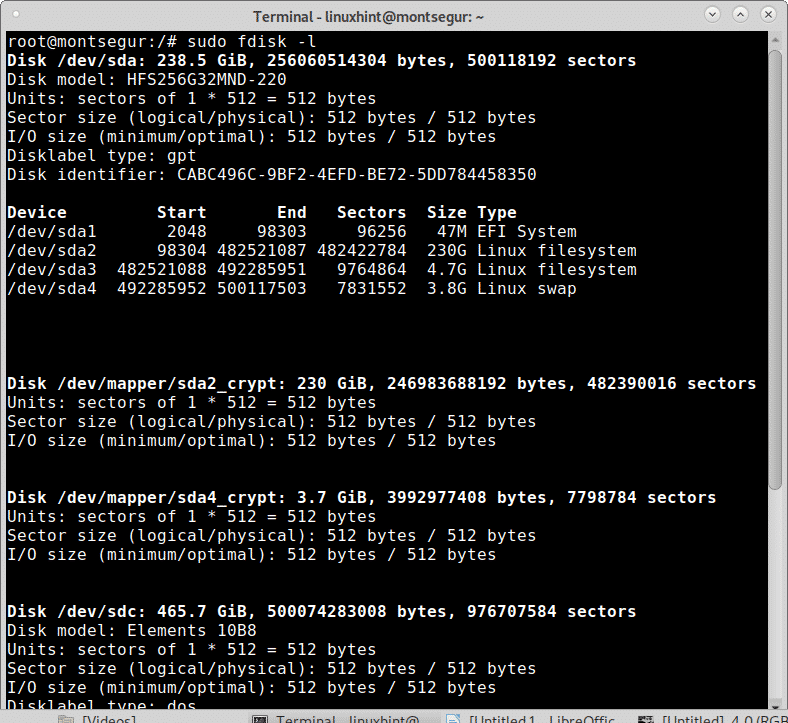
In the first column you can see all the connected devices, in the image above you can see 3 devices: sda, sdc and sdd. Lets see some information on each.
Lsblk, The column NAME:
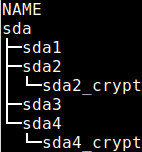
The NAME column shows the name of each disk device and partition. As you can see in the extract of the column below the disk SDA contains 4 partitions: sda1, sda2, sda3 and sda4. You can ignore the “_crypt_” for now.
The second listed disk device is sdc with only one partition, sdc1.
The second listed disk device is sdd with only one partition, sdd1.
The last listed device is the DVD or CDROM:
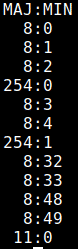
Lsblk, The column MAJ:MIN:
Following the column NAME there is the column MAJ:MIN is the internal identificator for each device the kernel uses according to the device type.
Lsblk, The column RM:
The column RM shows if the device is removable (where 1 yes and 0 no), in this case last 2 disk are external and the last device is the DVD.
Lsblk, The column SIZE:
The column SIZE displays the size of each of the disk devices listed.
Lsblk, The column RO:
The column RO means Read Only, being 1 positive and 0 negative, if 0 then devices are not read only, if 1, they are read-only.
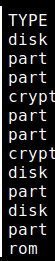
Lsblk, The column TYPE:
The column TYPE displays the type of device such as devices, partitions, optical devices, encrypted partitions and more.
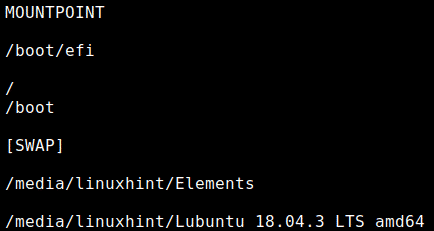
Lsblk, The column MOUNTPOINT:
The column MOUNTPOINT shows the mount point of each device or partition, the next image shows the partitions of the device sda.
The screenshot below shows an efi partition belonging to sda1, the encrypted sda2 root partition, the sda3 for boot and an encrypted sda4 SWAP.
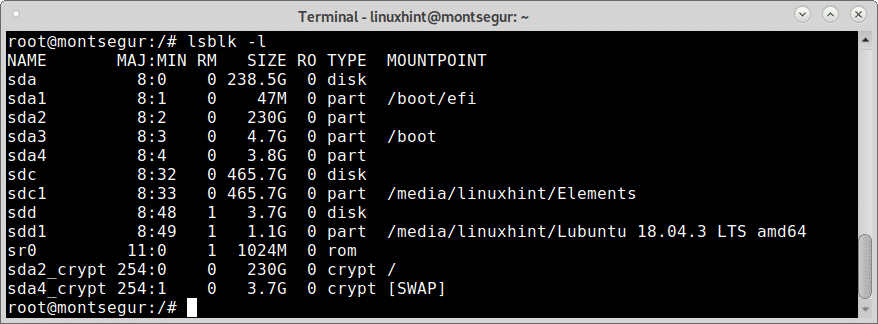
The flag -l will show the devices and partition as a list rather than as tree:
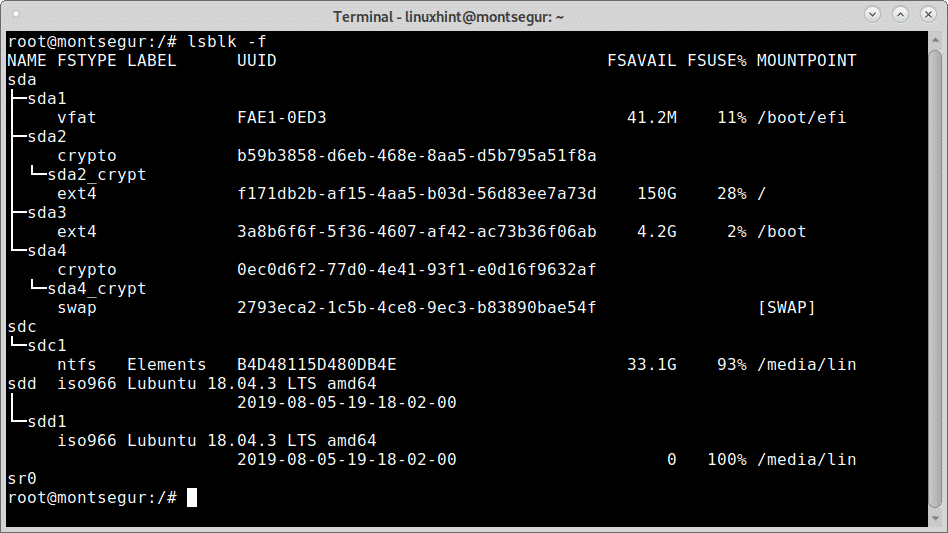
The flag -f instructs lsblk to inform the filesystem of each partition:
Additional flags for the command lsblk are available and explained in the man page which you can also access at https://linux.die.net/man/8/lsblk.
Listing disk devices in Linux with alternative methods: fdisk and fstab
While the correct way to list disk devices in Linux is using the command lsblk, other options are available.
The first one to try is fdisk, to list all block devices with fdisk run:
How to show free and used space in Linux disk devices
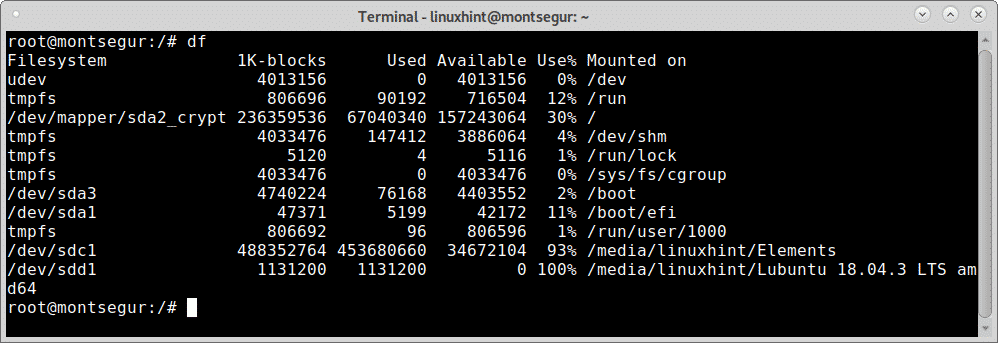
Additionally to listing your storage devices you may need to show the free and used space, this can be achieved using the command df.
As you see in the screenshot below, the availability of space of all disks formerly listed is now displayed.
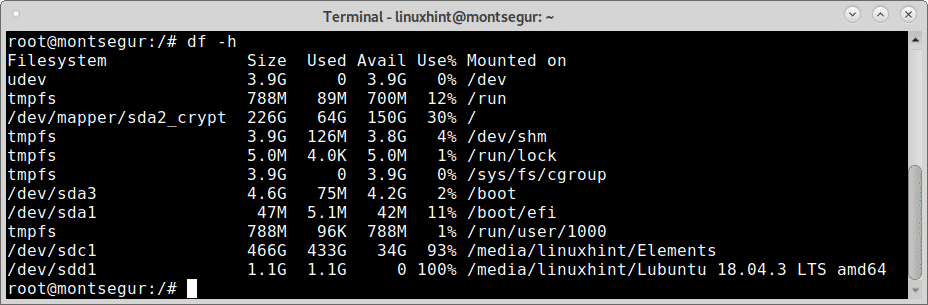
The command df allows you to easily check each partition identified both by its device name or its mountpoint, yet, the -h option makes it easier to be readed by humans.
For example the image above shows the partition /dev/sda2_crypt which is the root mount point / has 150 GB available and 64 GB used.