With the implementation of floating-point infinities, the infinity expands to the constant expression of float type data type, which evaluates to unsigned as well as positive infinity. On the other hand, the execution doesn’t care about floating infinities, and macro infinity enlarges the optimistic worth that insured to run-off a float data type at compile-time.
Assign Infinity value to a variable:
If we need infinity, use double or floating-point numeric values; you can easily get infinity. If the execution helps the double data-type infinities, the macro INFINITY develops to the continual appearance of type double, which estimates the positive and unidentified infinity. Look at this example:
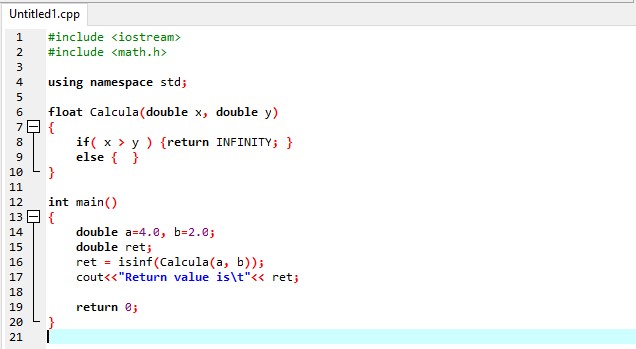
#include <math.h>
float Calcula(double x, double y)
{
if( x >y ) {return INFINITY; }
else { /* your else if you have one */ }
}
int main()
{
double a=4.0, b=2.0;
double ret;
ret = isinf(Calcula(a, b));
cout<<"Return value is %f"<<ret;
return 0;
}
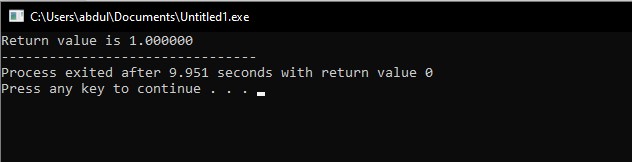
We use a header file. ‘#include <iostream>and #include <math.h>which describe one macro and several type of mathematical functions. This library contains all functions which we need in the library that take return double as a result that was taken double as an argument and as you can see in the code. When the consequence of an object is not representable as a floating numeric value, we use the macro. In the main body, we initialized variables with the data type of the double having name “a”, “b”, and “ret” respectively. Then we assign a function of “isinf” to “ret” with the parameters of “a” and “b”. After that, we display the set.
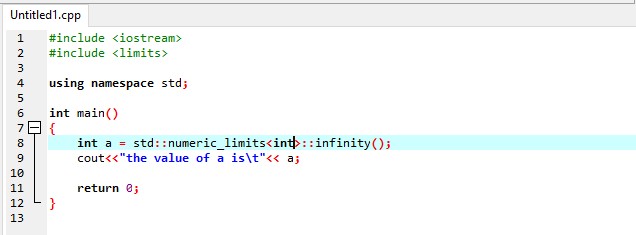
Setting an int Infinity:
Integers are inherently finite; that is why we cannot define them to a right infinity. The nearby value that we can get is by initializing an “int” to its extreme value. The closest we can get by setting a variable to the maximum value that is double “a = std: numeric_limits<int>:: max();”. Which would be 231-1 if it is 32 bits wide on our implementation. With this expression, we can assign this variable to the maximum value of int, which means it could be equal or greater than any other integer value.
#include <limits>
using namespace std;
int main()
{
int a = std::numeric_limits<int>::infinity();
cout<<"the value of a is\t"<<a;
return 0;
}
}
We integrate a header file #include <iostream>and #include <limit>. These type of libraries defines the elements with the features of arithmetic types. More in detail, it describes a numeric limit class pattern and a specialization for individuals of the types. In the main body of the code, we initialized a variable with integer data-type, assign it a numeric limit with int, and apply infinity at the end of the statement. It is also called positive infinity because the value of ‘a’ equals zero. Then we display the result as we said before that integers are not finite, and we can’t set it to a true infinity.
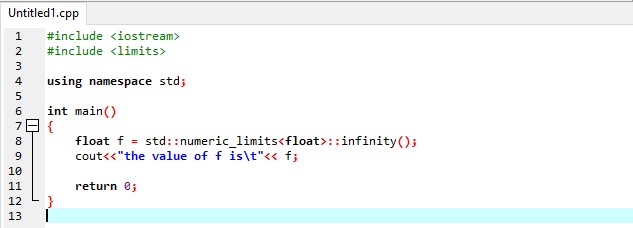
Setting a float Infinity:
The only true infinities in C++ are the floating-point data-types if your platform supports the concept of a float; as we mentioned before, if we need infinity, use a floating-point number type, like float and double we will get infinity as it shows in the following example.
#include <limits>
using namespace std;
int main()
{
float f = std::numeric_limits<float>::infinity();
cout<<"the value of f is\t"<<f;
return 0;
}
First of all, we use two header files ‘#include <iostream>and #include <limit>. Then we write the main body of the code, where we initialized a variable with float data-type and assigned it a numeric limit with float; you can also use double at the place of float and get infinity. We also apply infinity at the end by assigning the limit with float data type. Then we print the output, and you can see floating types are true infinities.
Negative Infinity:
The negative infinity result is less than zero so for the integer data-type, it does not have an infinity value rather we can use “std::numaric_limits<double>:: infinity();” to get the maximum value of an integer.
#include <limits>
using namespace std;
int main()
{
int b = std::numeric_limits<double>::infinity();
cout<<"the value of b is\t"<<b;
return 0;
}
First of all, we wrote two header files ‘#include <iostream>and #include <limit>. Then we start the main body of the code, where we initialized a variable with float data-type and assigned it a numeric limit with float; you can also use double at the place of float and get infinity. By assigning the limit with the float data type, we also apply infinity at the end. Then we print the output, and you can see that integer data types with double or float data types result in the negative limit of the integer value.
Conclusion:
In this article, we define the infinity and the syntax of the infinity with the different data types. We discuss that infinity cannot be defined solely in terms of number or the combination of the numeric values with the examples of different types of infinity. We conclude that integer data type is not good for infinity, but float and double are the suitable data types for infinity.