How to use Nohup in Linux

Imagine if a critical process is running on your system and taking a long time. Suddenly you need to log out of your system. If you log out, your processes will stop, and you will certainly want to avoid this. If you want your running process to be continued without any interruption, then you need nohup command.

Nohup (stands for no hangup) is a command that ignores the HUP signal. You might be wondering what the HUP signal is. It is basically a signal that is delivered to a process when its associated shell is terminated. Usually, when we log out, then all the running programs and processes are hangup or stopped. If we want to continue running the process even after logout or disconnection from the current shell, we can use the nohup command. It makes the processes immune to HUP signals in order to make the program run even after log out. With nohup, you will no longer need to login for a long time just to wait for the process to be completed.

In this article, we will explain how to use the Nohup command in different scenarios in Linux.

Nohup Command Syntax

To use the nohup command, syntax is:

or

To find the help regarding the nohup command, use the following command:

To find the version information of nohup, use the following command:

Start a process using Nohup

If you want to keep a command or process running even if you exit the shell, use the nohup followed by the command to execute:

Once you run the above command, all the output, along with the error messages, will be added to the nohup.out file in the Home directory or in the current directory. Now, if the shell is closed or you log out, the above-executed command will not be terminated.

Redirect output to different file

By default, the output of nouhup command is added to the nohup.out file. To redirect this output to some other file, use > redirector operator followed by the name of the specific file. For instance, we have used the following command to save the output of nohup command to a new file named “myscript.sh”.

Start a process in the background using Nohup

To start and put the process in the background, you will need to use the nohup as follows:

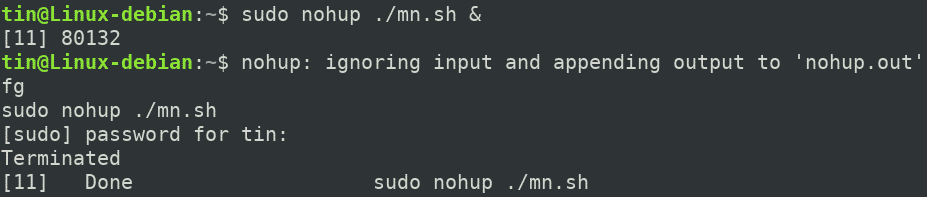
The & symbol tells the shell to run the command in the background. It is similar to the above nohup command except that when the session ends, it returns immediately to the shell prompt. To bring it back to the forefront, use  the “fg” command.

The output of all the commands you execute will be appended to the nohup.out file. You can view this file using the cat nohup command in the Terminal. The number 80132 in the above screenshot indicates the process Identification number (PID) of the process running in the background.

Start multiple processes in the background using Nohup

You can run multiple commands in the background by using the nohup command. In the following example, mkdir, ping, and ls commands are executed in the background by using nohup command.

Terminate process running in the background

To terminate a process running in the background, use the kill command as follows:

You will find the PID of a process when using the nohup with “&”. Another way to find PID is through the pgrep –a command. For instance, if you have run the Ping command with nohup, it’ll keep running in the background even if you close the shell. Now in this case, to find the PID of a Ping process running in the background, use this command:

It will list all the processes associated with the Ping command.

Now to terminate the Ping process running in the background, use the kill command as follows:$ kill -9 80928So, this was the brief introduction of nohup command in Linux. Nohup command is used to prevent an important process from being terminated when you log out or close the session. It helps a lot when you are running a process, especially scripts that take a long time to complete.